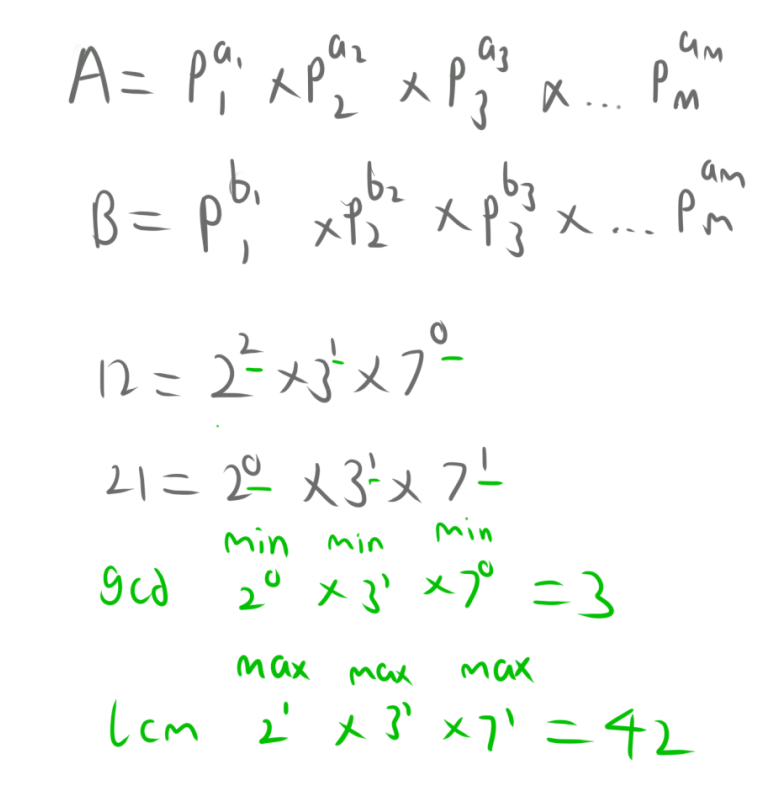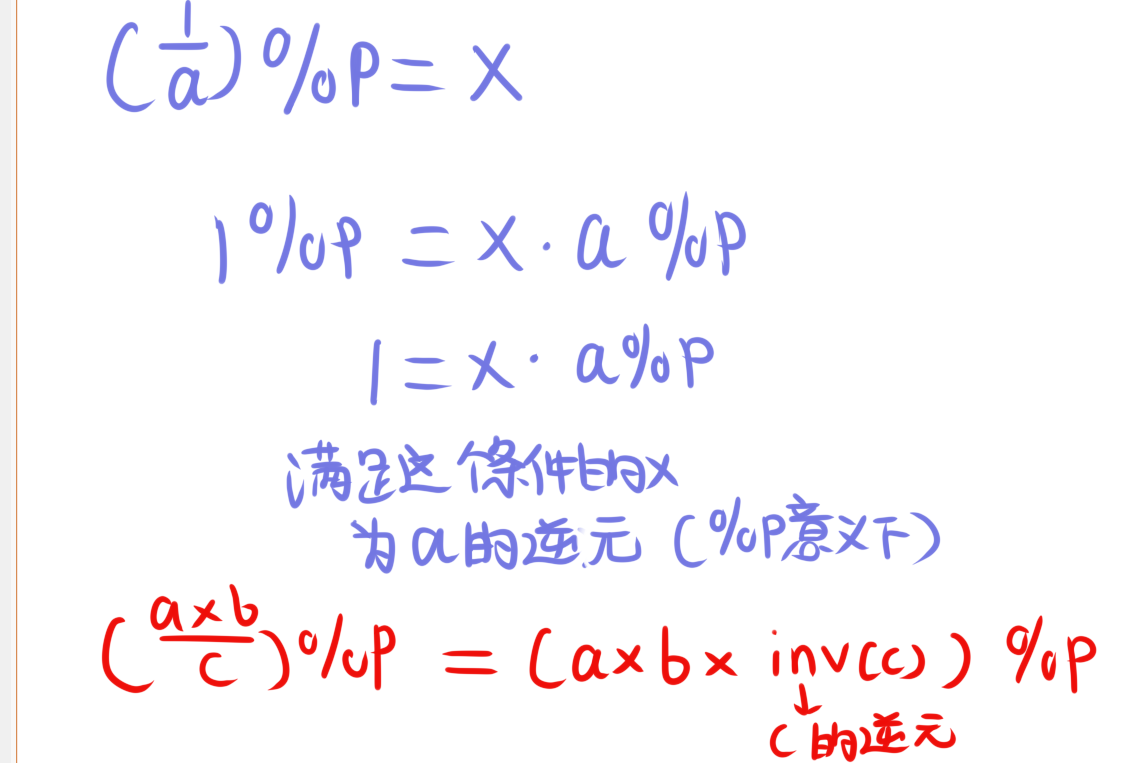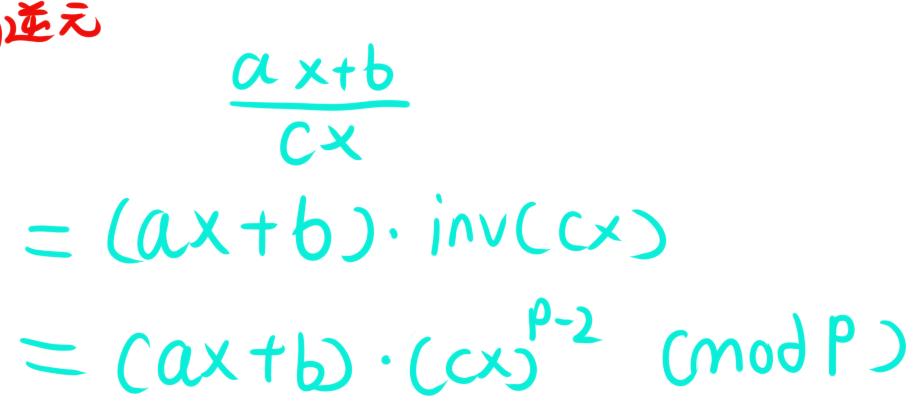前言
学习网站:Starrycoding
常用算法wiki:OI wiki
埃式筛
埃式筛是一种用于快速找到一定范围内所有质数的算法。它的基本思想是从2开始,将每个质数的倍数都标记成合数,直到筛完所有小于等于n的数。
具体来说,算法的步骤如下:
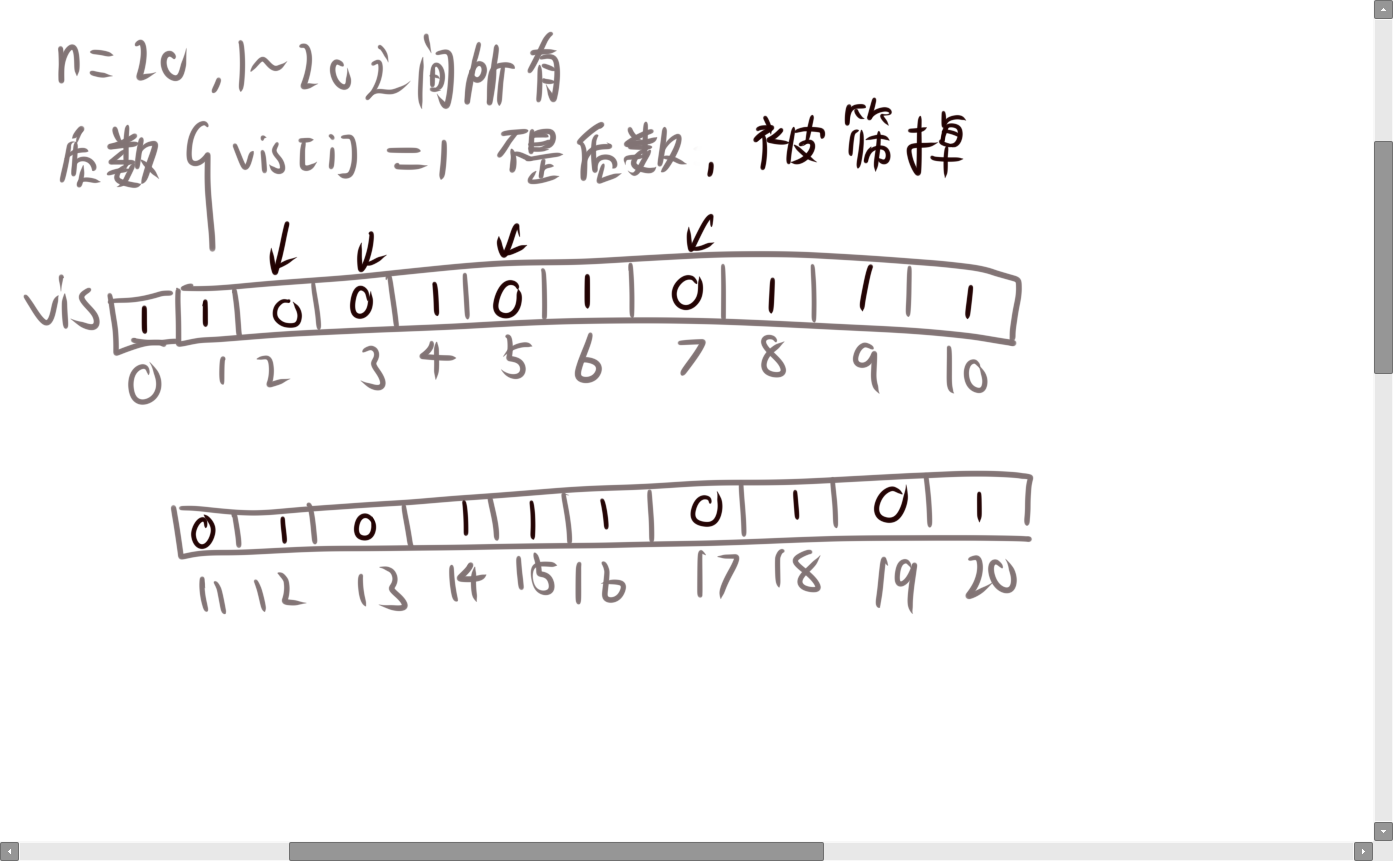
- 初始化一个vis数组,将所有元素标记为0,刚开始我们认为所有数都是质数。而1代表不是质数。然后我们初始化将0,1标记为1。
- 从2开始判断是不是质数,如果是质数,就将它的倍数都标记为1.
- 然后我们判断下一个数是不是质数,如果是质数,就将它的倍数都标记为1.
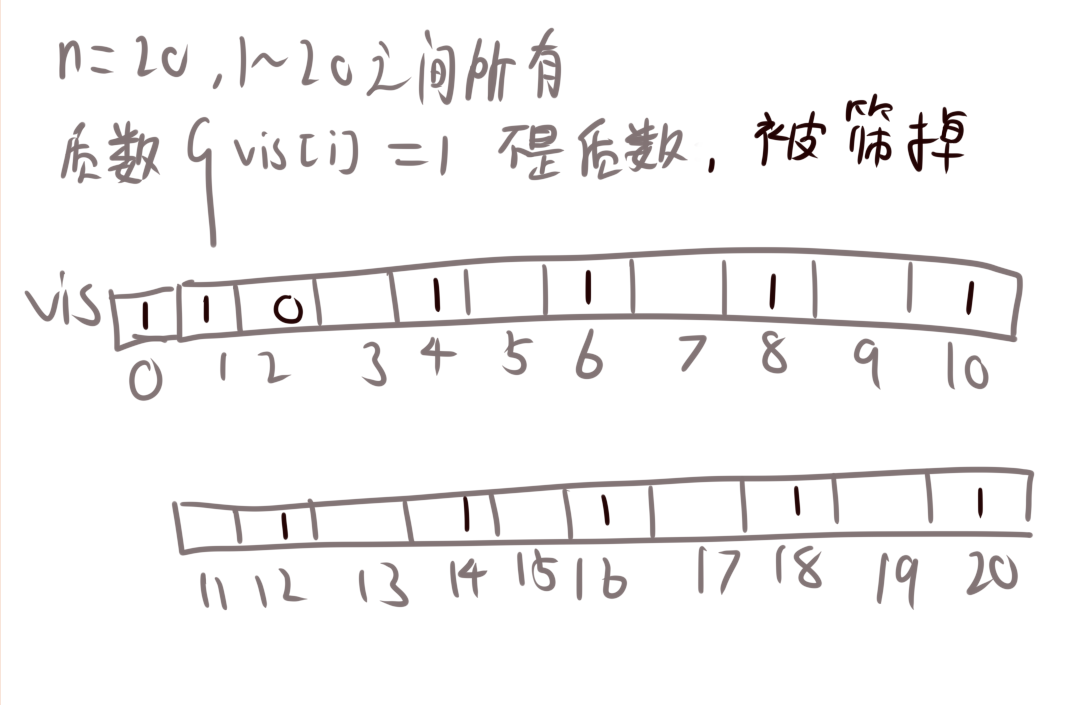
最终vis数组中为0的数就是质数。
例题
P43 【模板】埃氏筛法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 9;
bitset<N> vis;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
vis[0] = true;
vis[1] = true;
for (int i = 2; i <= n; i++)
{
if (!vis[i])
{
for (int j = i * 2; j <= n; j += i) // 从i的2倍开始,每次加i
{
vis[j] = true;
}
}
}
for (int i = 2; i <= n; i++)
{
if (!vis[i])
{
cout << i << " ";
}
}
cout << "\n";
return 0;
}
|
我们可以分析下这个算法的时间复杂度。

如图,我们可以看到,埃式筛枚举倍数的方法使得这个循环的时间复杂度为$O(n\log n)$。于是总共就是$O(n\log\log n)$。
顺带一提,枚举倍数我们也可以优化,将循环改为这样:
1
2
3
4
5
6
7
8
9
10
|
for (int i = 2; i <= n; i++)
{
if (!vis[i])
{
for (ll j = 1ll*i * i; j <= n; j += i)
{
vis[j] = true;
}
}
}
|
初始化j为i的平方,不会影响结果(我们可以自己代数字看一下,假设i很大,那么在到i之前,$2\times i$,$3\times i$,$4\times i$等倍数肯定已经在枚举到$2,3$等数的时候被标记过了)。
最终代码就是:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 9;
typedef long long ll;
bitset<N> vis;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
vis[0] = true;
vis[1] = true;
for (int i = 2; i <= n; i++)
{
if (!vis[i])
{
for (ll j = 1ll*i * i; j <= n; j += i)
{
vis[j] = true;
}
}
}
for (int i = 2; i <= n; i++)
{
if (!vis[i])
{
cout << i << " ";
}
}
cout << "\n";
return 0;
}
|
gcd和lcm
gcd是最大公因数,lcm是最小公倍数。

关于gcd和lcm,我们首要要知道一个定理,叫做惟一分解定理
该定理断言:任何一个大于1的整数n都可以分解成若干个素因数的连乘积,如果不计各个素因数的顺序,那么这种分解是惟一的
$$N={p_1}^{a_1} \times {p_2}^{a_2} \times {p_3}^{a_3} \times {p_4}^{a_4} ....\times {p_m}^{a_m} $$其中$p_i$是素数,$a_i$是正整数。
而gcd和lcm也与这个定理有关。
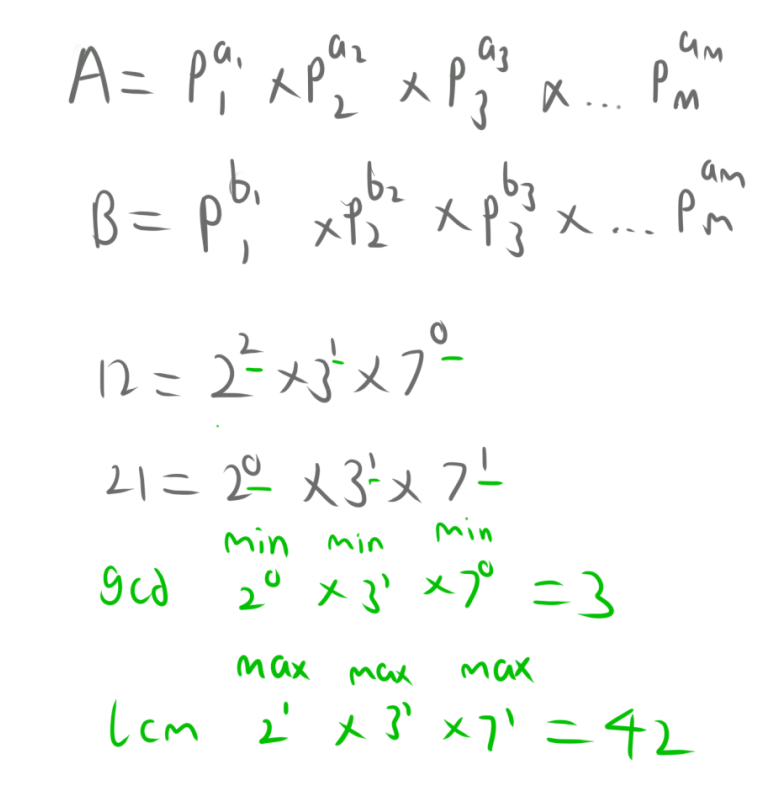
如图,将两个数的质因数分解,保证他们的因子全部相同,那么他们的gcd就是这些因子的最小值乘积,而lcm就是这些因子的最大值乘积。
同时,我们可以发现$gcd(a,b)\times lcm(a,b)=a\times b$。
于是,我们得出了gcd与lcm的关系,那么我们只要求出gcd或lcm,另一个就可以通过公式得出。
通常,我们会使用辗转相除法来求gcd。然后再得出lcm。

辗转相除法的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b)
{
if (b == 0)
{
return a;
}
else
{
return gcd(b, a % b);
}
}
|
例题
P65 【模板】gcd和lcm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b)
{
if (b == 0)
{
return a;
}
else
{
return gcd(b, a % b);
}
}
ll lcm(ll a, ll b)
{
return (a / gcd(a, b)) * b; // 注意这里要先除再乘,防止溢出
}
void solve()
{
ll a, b;
cin >> a >> b;
cout << gcd(a, b) << " " << lcm(a, b) << "\n";
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while (t--)
{
solve();
}
}
|
快速幂
快速幂是一种用于计算幂运算的算法,它可以在$O(\log n)$的时间复杂度内计算出$a^n$的值。
快速幂的基本思想是将幂运算转化为二进制数的形式,然后利用二进制数的性质来计算幂运算。

如图,假设我们要计算$a^n$,我们可以将n转化为二进制数,然后将二进制数转化为幂运算的形式。
例如,$a^7$可以转化为$a^4\times a^2\times a^1$。
7的二进制为111,我们对应只要有1就乘上a,并且数字a每次都要自乘,这样就可以得到$a^7$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
ll qmi(ll a, ll b, ll c)
{
ll res = 1;
while (b != 0)
{
if (b & 1) // 如果b的二进制最后一位为1
{
res = res * a;
}
a = a * a; // 每次循环a都要翻倍
b >>= 1;
}
return res;
}
|
需要注意的是,假如题目有运用快速幂,那么题目绝对是要取模的,因为出题人肯定要想办法避免数据溢出。
这里要指出取模运算对于$+-\times$这三种运算是封闭的,也就是说,$(a+b)%m=(a%m+b%m)%m$,$(a\times b)%m=(a%m\times b%m)%m$。
我们可以看出在最终结果需要取模时,我们可以将每一步都取模,却不会影响最终结果。
例题
P66 【模板】快速幂
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll qmi(ll a, ll b, ll c)
{
ll res = 1;
while (b != 0)
{
if (b & 1) // 如果b的二进制最后一位为1
{
res = res * a % c;
}
a = a * a % c; // 每次循环a都要翻倍
b >>= 1;
}
return res;
}
void solve()
{
ll a, b, c;
cin >> a >> b >> c;
cout << qmi(a, b, c) << "\n";
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
|
乘法逆元
乘法逆元是数论里的知识
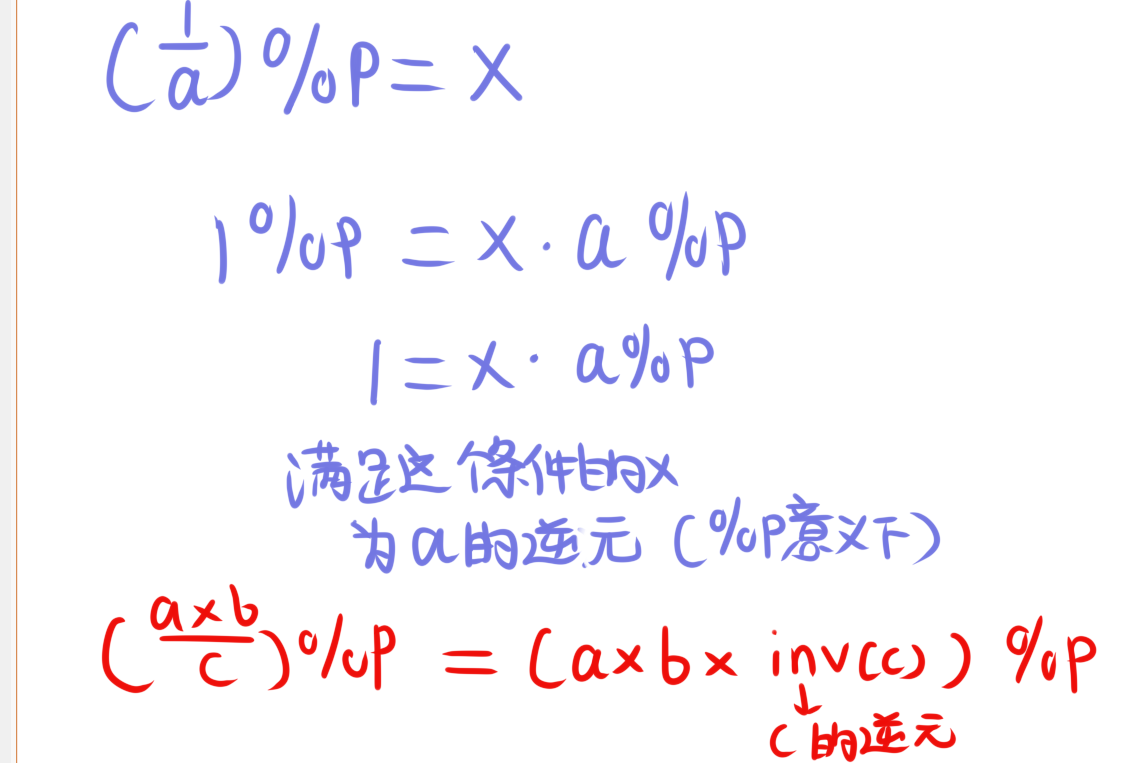
假设一个方程为$\frac{1}{a} \bmod b = x$
我们可以将其转化为$x\times a \bmod b = 1$。
其中的这个$x$为a的逆元($\bmod b$ 意义下)。
即
$$\frac{a\times b}{c} \mod d = (a\times b \times inv(c)) \mod d$$其中的$inv(c)$为c的逆元。
需要注意的是,这个逆元绝对是要有取模参与的。
接着我们还要知道费马小定理。

费马小定理告诉我们
当$p$为质数时(任意一个质数都行),始终有
$$a^{p-1} \bmod p = 1$$则有
$$a^{p-1} \equiv 1 \pmod{p} $$$$a \times a^{p-2} \equiv 1 \pmod{p} $$$$a^{p-2} \equiv \frac{1}{a} \pmod{p} $$$$a^{p-2} \equiv inv(a) \pmod{p} $$所以,我们就可以用快速幂加上取模来求逆元了(很明显,要求逆元题目就会规定一个质数来让你取模,常见的有$998244353$,$1e9+7$)
例题
P44 【模板】乘法逆元
分析:
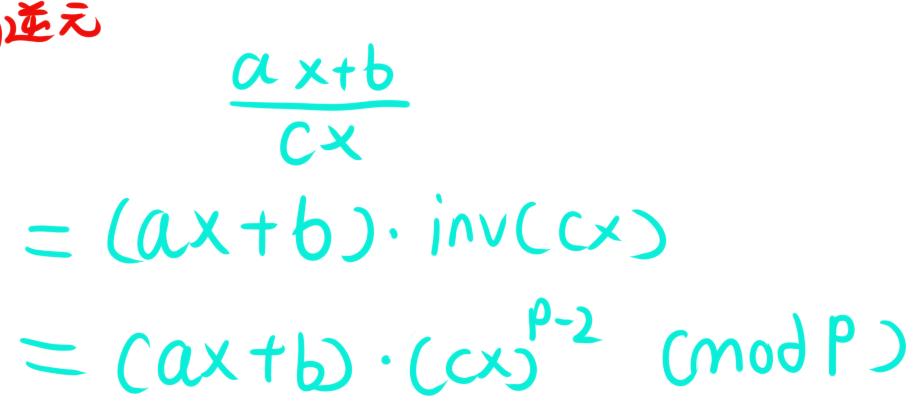
如图,我们可以把
$$\frac{a\times x + b}{c\times x} $$转化为
$$(a\times x +b) \times (c\times x)^{p-2} \bmod p$$如此就可以求出题目的函数值,并且不会数据溢出
假如不用这种方法,有除法存在会导致我们没法使用取模来使数据不溢出
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p = 998244353;
ll qmi(ll a, ll b)
{
ll res = 1;
while (b != 0)
{
if (b & 1) // 如果b的二进制最后一位为1
{
res = res * a % p;
}
a = a * a % p; // 每次循环a都要翻倍
b >>= 1;
}
return res;
}
ll inv(ll x)
{
return qmi(x, p - 2);
}
ll f(ll x, ll a, ll b, ll c)
{
return ((a * x % p + b) % p) * inv(c * x % p) % p;
}
void solve()
{
ll a, b, c, q;
cin >> a >> b >> c >> q;
while (q--)
{
ll x;
cin >> x;
cout << f(x, a, b, c) << "\n";
}
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
|