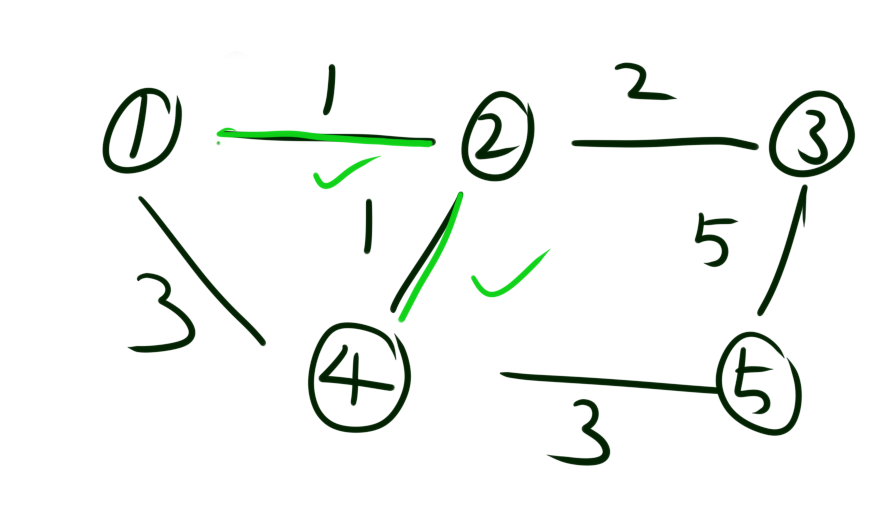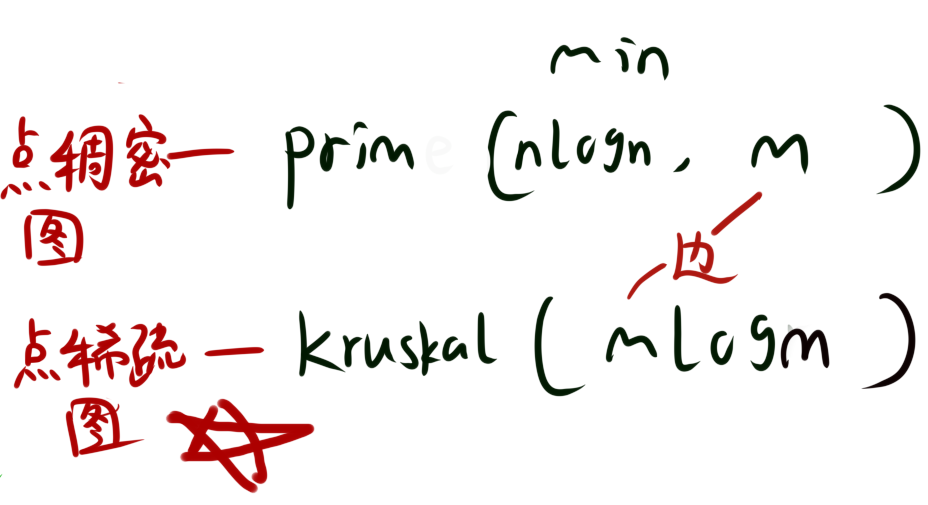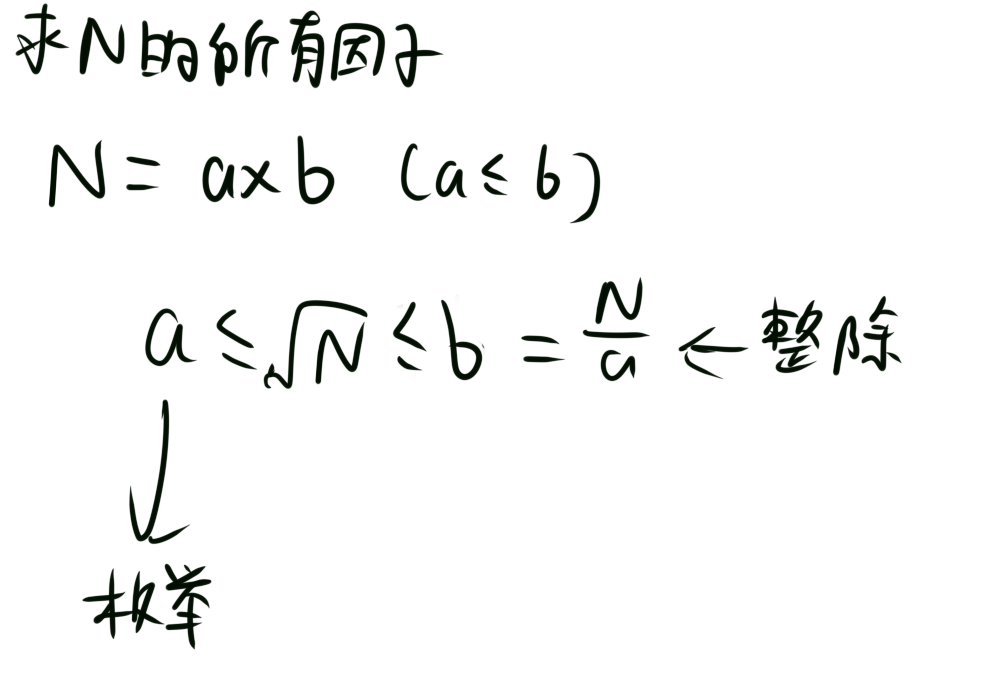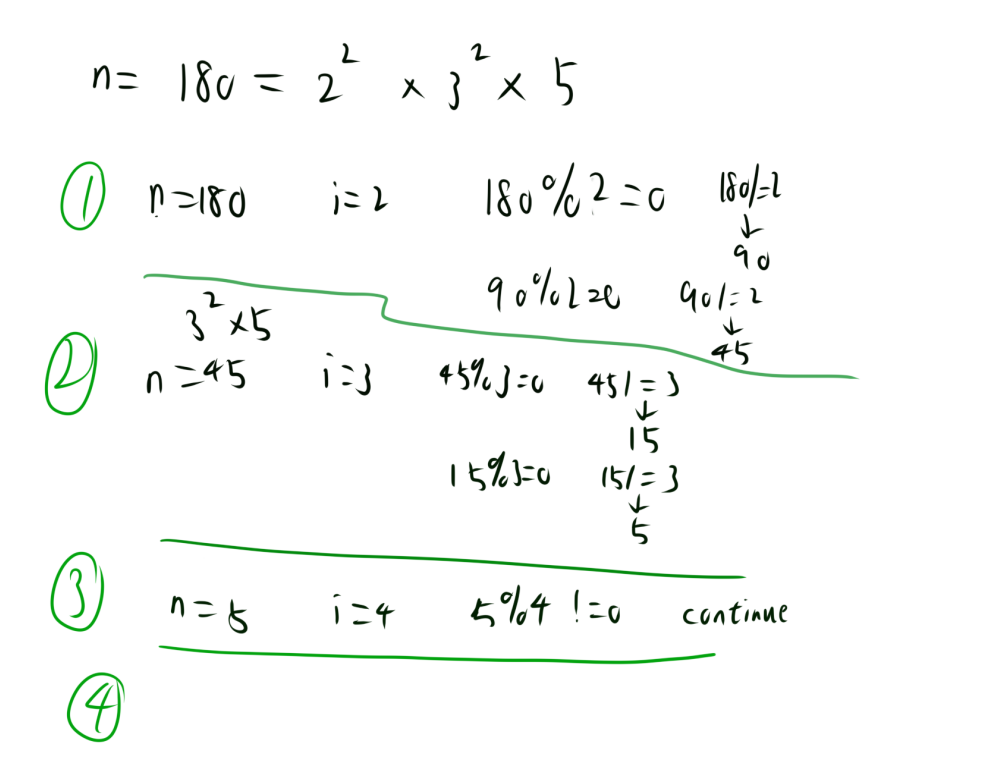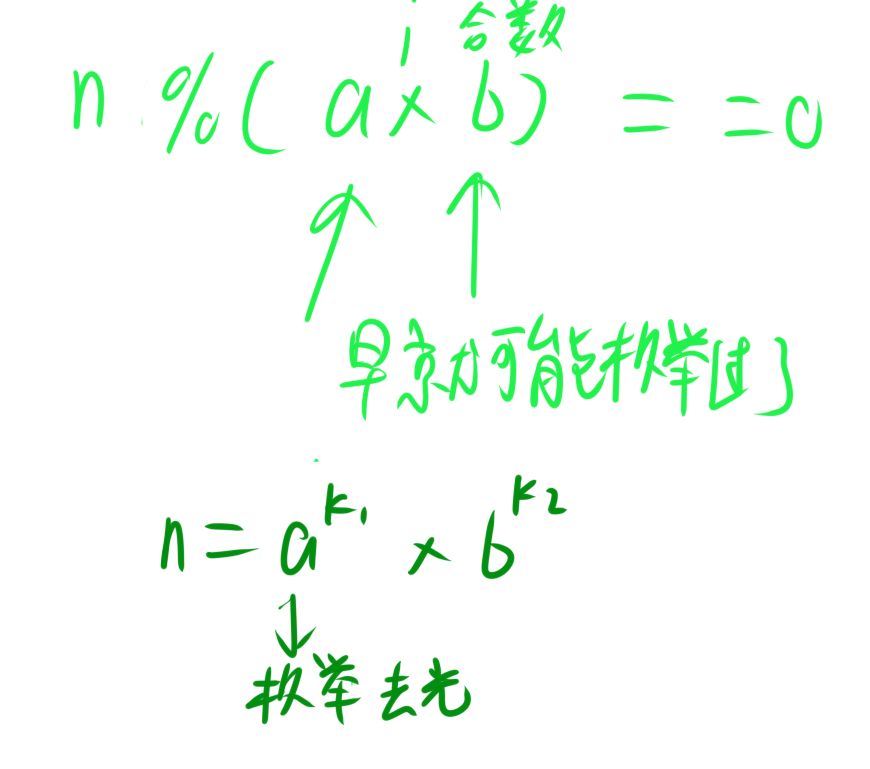前言
学习网站:Starrycoding
最小生成树
最小生成树用于处理无向图的最小权值和。
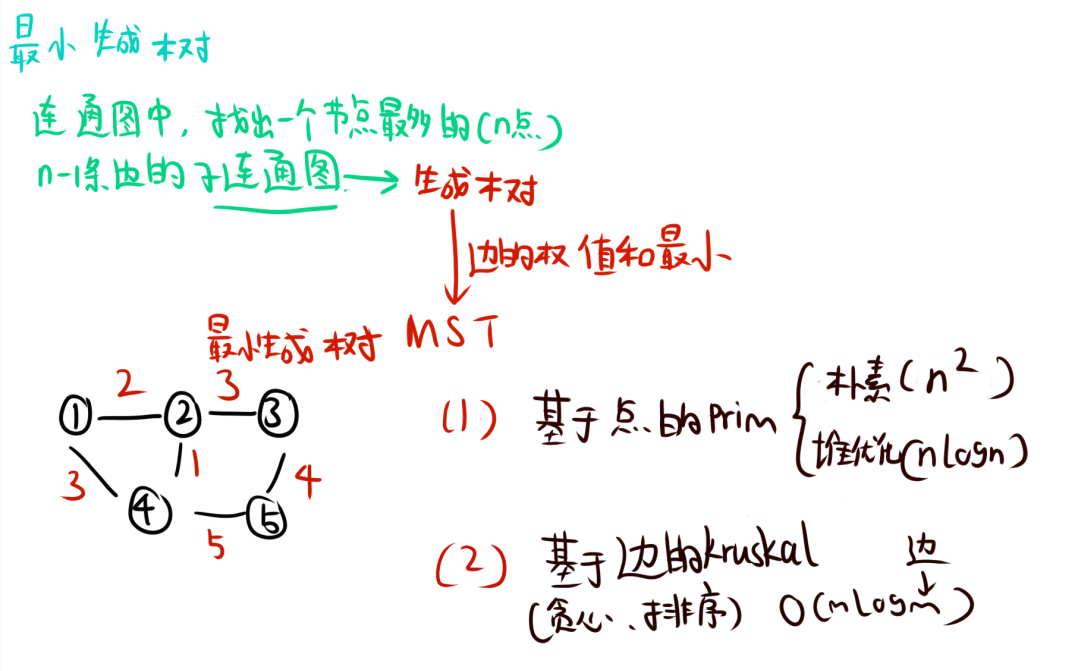
最小生成树的实现有两种方法:
Prim算法
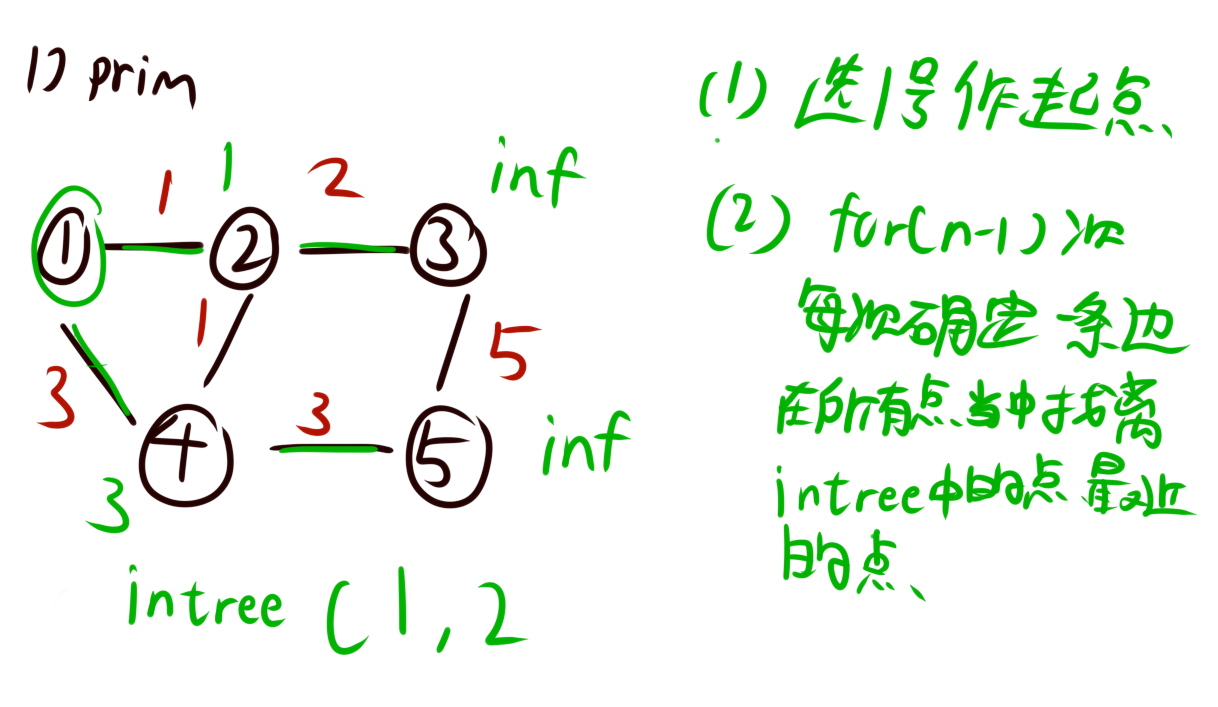
- 对于一个无向图,我们选择一个点作为起点,一般选点1。(方便枚举)
- 我们用一个数组dist[]来记录所有点到起点的距离,初始化为正无穷。
- 我们用一个bool数组st[]来记录这个点是否已经被加入到生成树中。
- 我们用一个循环,每次循环中找到不在生成树中的距离起点最近的点,将这个点加入到生成树中。
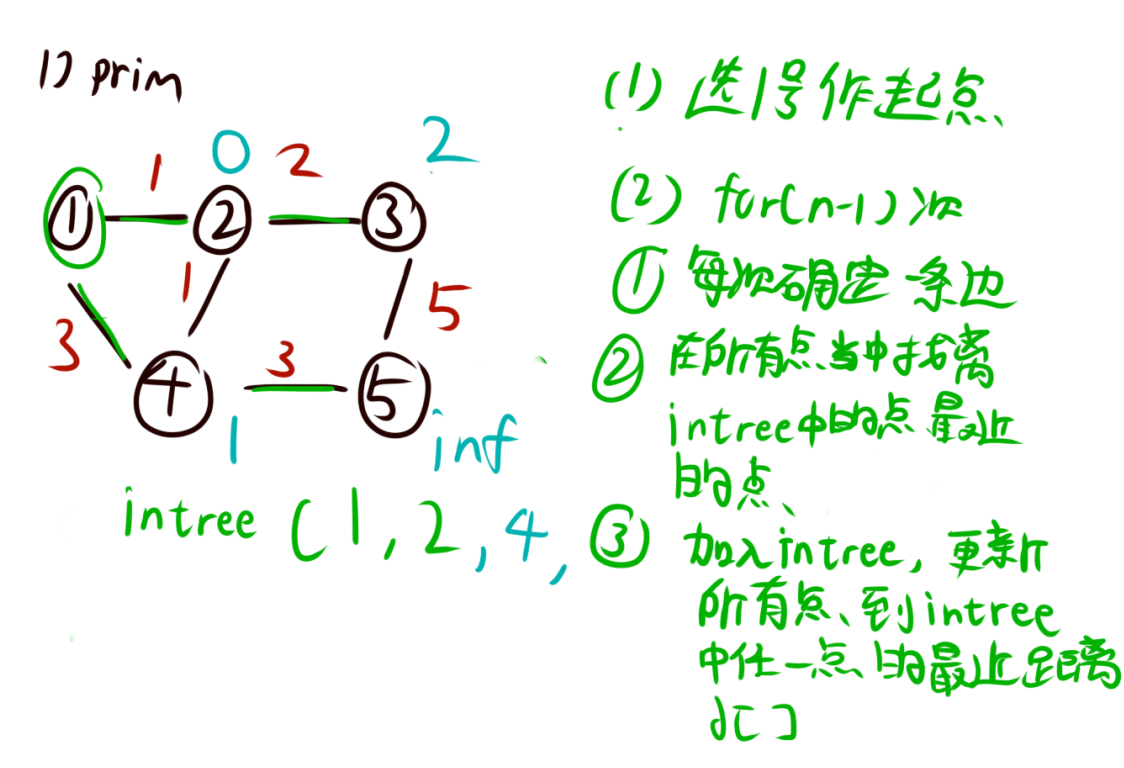
- 当这个点加入进去,我们需要更新dist[]数组,将这个点的所有邻边的距离起点的距离更新一下。并且这个点的dist[]=0。
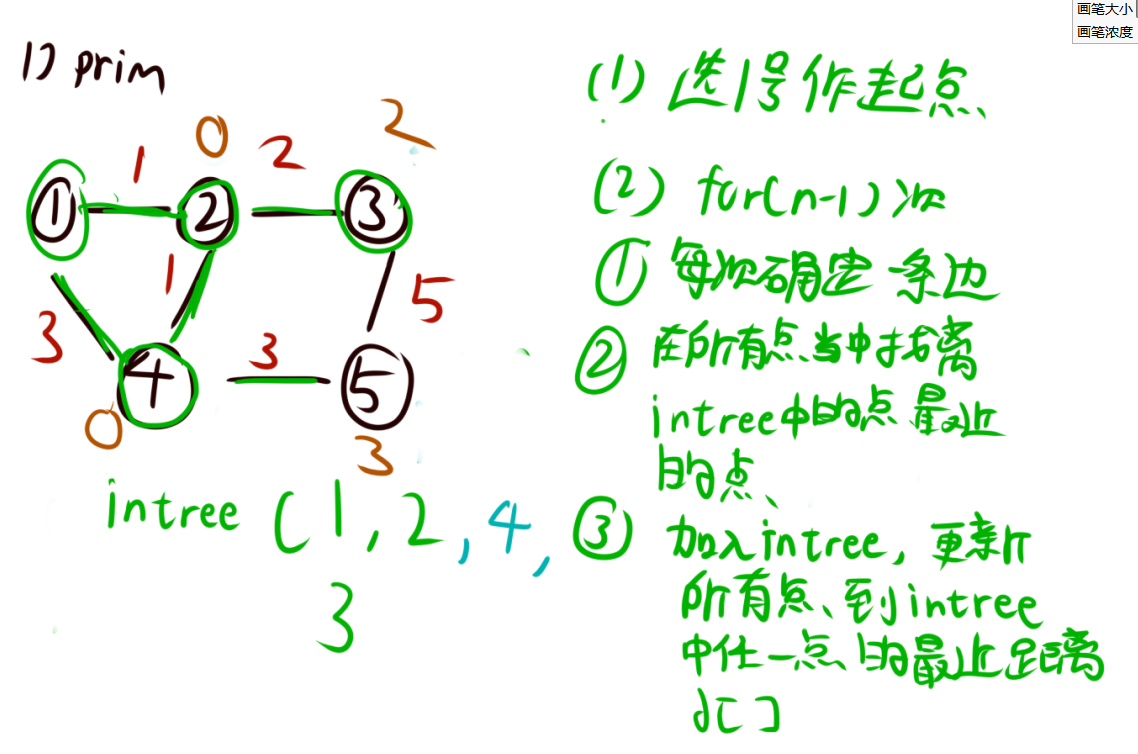

根据这个思路,我们可以写出朴素的Prim算法。时间复杂度为$O(n^2)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 9; //朴素算法能处理的范围很小
typedef long long ll;
ll a[N][N], d[N];
bitset<N> intree;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m;
cin >> n >> m;
memset(a, 0x3f, sizeof(a));
memset(d, 0x3f, sizeof(d));
for (int i = 1; i <= n; i++)
{
a[i][i] = 0; //自己到自己的距离为0
}
for (int i = 1; i <= m; i++)
{
ll u, v, w;
cin >> u >> v >> w;
a[u][v] = min(a[u][v], w); //用邻接表存无向图
a[v][u] = min(a[v][u], w);
}
ll ans = 0;
for (int i = 1; i <= n; i++)
{
int u = 1; // u就是我们要找的那个距离intree中的点最近的那个点,一开始就从1开始。
for (int j = 1; j <= n; j++)
{
if (intree[u] || (!intree[j] && d[j] < d[u]))
{
u = j;
}
}
if (i != 1)
ans += d[u]; // 我们要把所有的权值加起来,但是第一个点是没有权值的,所以我们要特判一下。
intree[u] = true;
d[u] = 0;
for (int j = 1; j <= n; j++) // 每次生成树进入一个点都更新dist[]数组
{
if (intree[j])
continue;
d[j] = min(d[j], a[u][j]);
}
}
cout << ans << "\n";
return 0;
}
|
例题1
P72 【模板】最小生成树
分析:
题目的数据范围在$10^5$,所以我们用朴素的Prim算法是不能过的。我们该如何优化呢,观察循环,我们可以发现,我们每次循环中都要找到不在生成树中的距离起点最近的点,这个点我们可以用一个优先队列来维护,每次取出堆顶元素即可。这样我们就可以将时间复杂度优化到$O(nlogn)$。(和dijkstra很像)
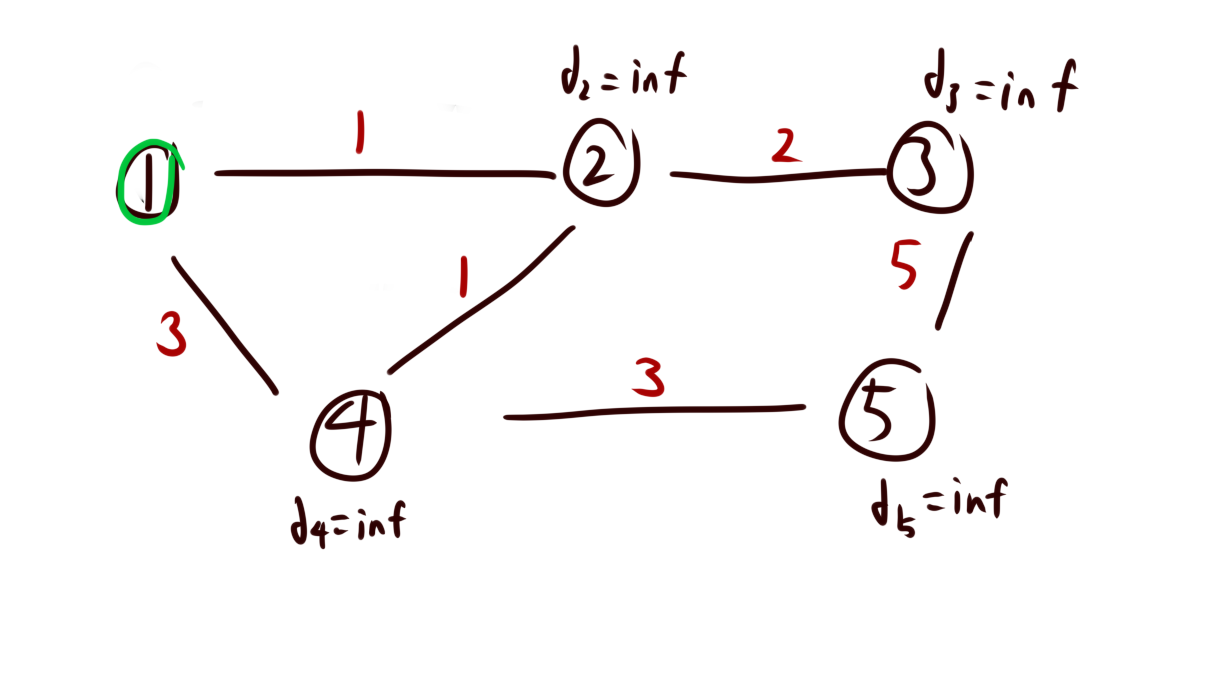
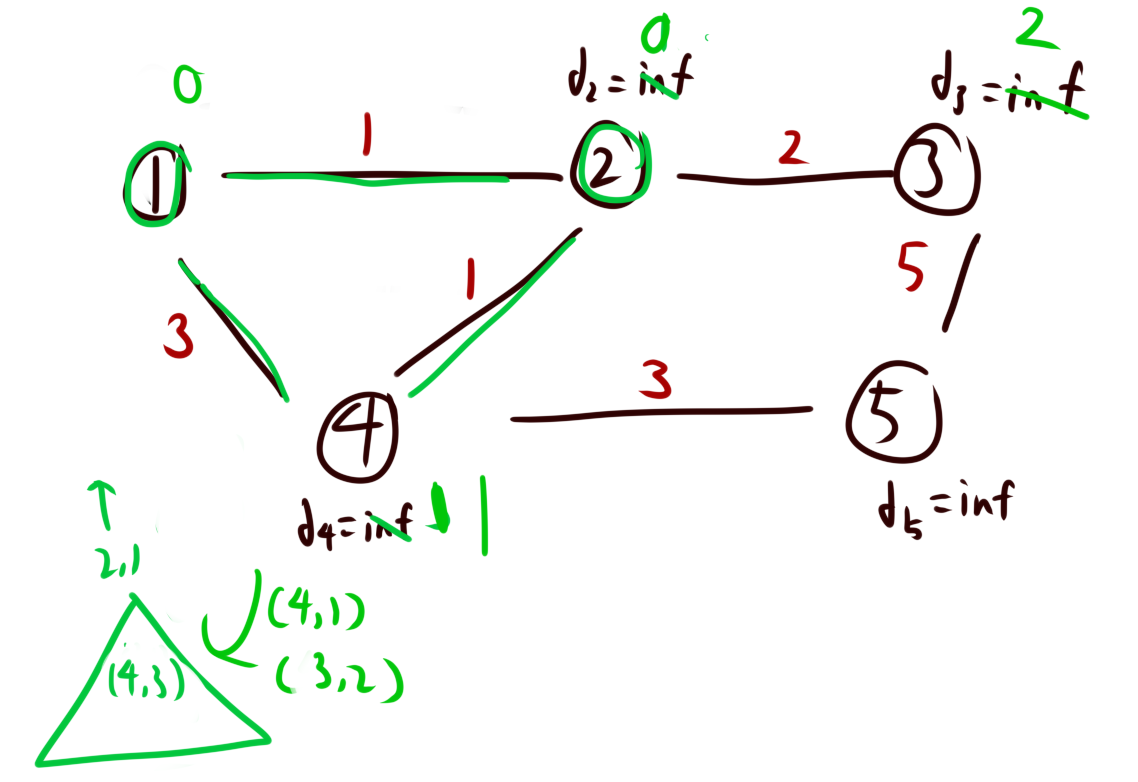
至于我们该如何入队,我们可以用一个循环来实现,每次循环中,我们将这个点的所有邻点的距离起点的距离更新一下。并且这个点的dist[]=0。假如邻点的dist[]变化了,那么他就有可能成为最近点,直接将他入队即可。
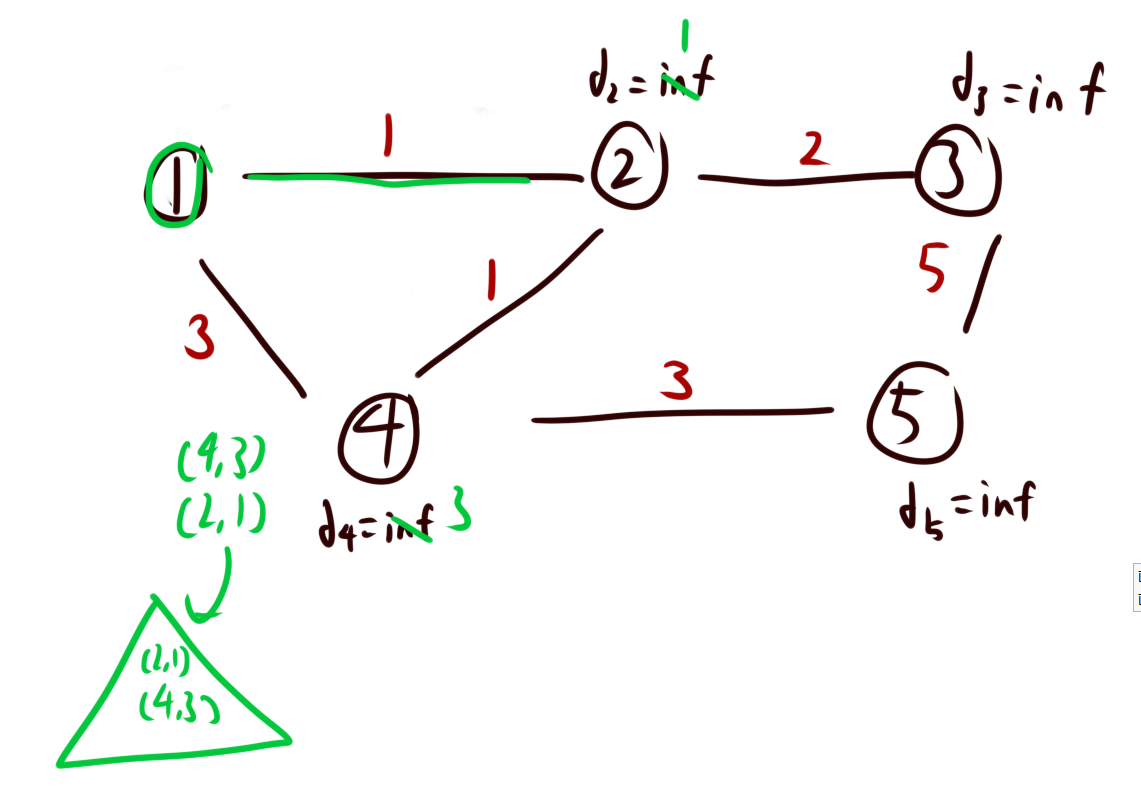
之后我们就用优先队列来帮我们判断最近点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
|
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
typedef long long ll;
struct node
{
ll x;
ll w;
bool operator<(const node &b) const // 权值最小的优先,如果权值相同,那么用编号区分,编号小大无所谓
{
return w == b.w ? x < b.x : w > b.w;
}
};
vector<vector<node>> g(N, vector<node>());
bitset<N> intree;
ll d[N];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m;
cin >> n >> m;
memset(d, 0x3f, sizeof(d));
for (int i = 1; i <= m; i++)
{
ll u, v, w;
cin >> u >> v >> w;
g[u].push_back({v, w});
g[v].push_back({u, w});
}
ll ans = 0;
priority_queue<node> pq;
pq.push({1, 0});
d[1] = 0;
while (pq.size())
{
ll u = pq.top().x; // 取出来的点是距离当前intree中的点最近的一个
pq.pop();
if (intree[u])
{
continue;
}
intree[u] = true;
ans += d[u];
d[u] = 0;
// 枚举所有出边
for (auto &edge : g[u])
{
ll y = edge.x;
ll w = edge.w;
if (!intree[y] && w < d[y]) //我们要取的是最小的权值,大的就不用入队了,并且已经在生成树的点也是肯定不能进的.
{
d[y] = w;
pq.push({y, d[y]});
}
}
}
for (int i = 1; i <= n; i++) // 最后判断一下是否所有的点都在生成树中,如果有一个点不在生成树中,那么就不构成生成树了,输出-1。
{
if (!intree[i])
{
ans = -1;
break;
}
}
cout << ans << "\n";
return 0;
}
|
Kruskal算法

kruskal算法是基于边的算法,它的思想是根据权值从小到大将边进行联通(用并查集),如果这条边的两个点已经联通了,那么这条边就不能加入到生成树中。
这种算法就是一种贪心的算法,它的时间复杂度为$O(mlogm)$。m指的是边的数量。
下面演示一下kruskal算法的过程:
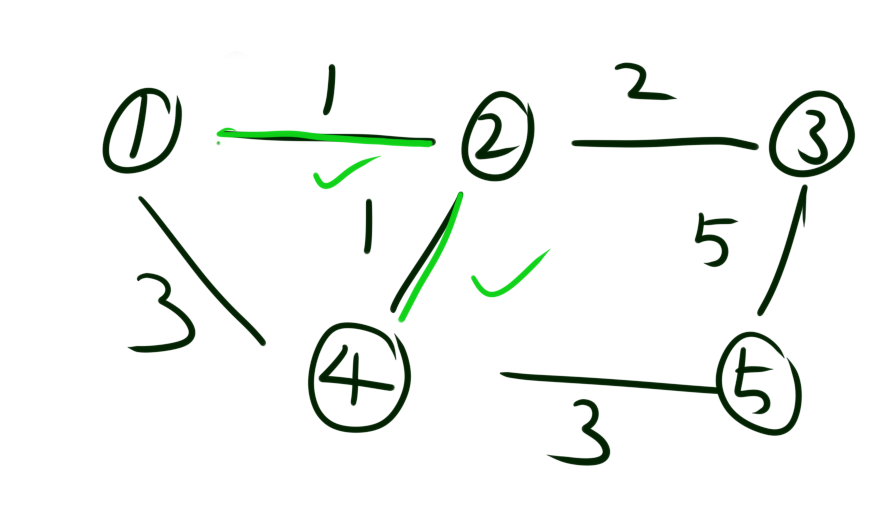
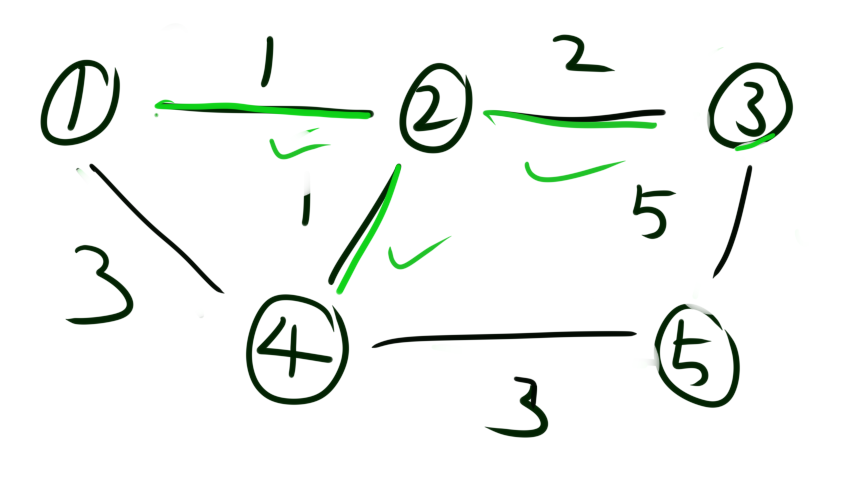
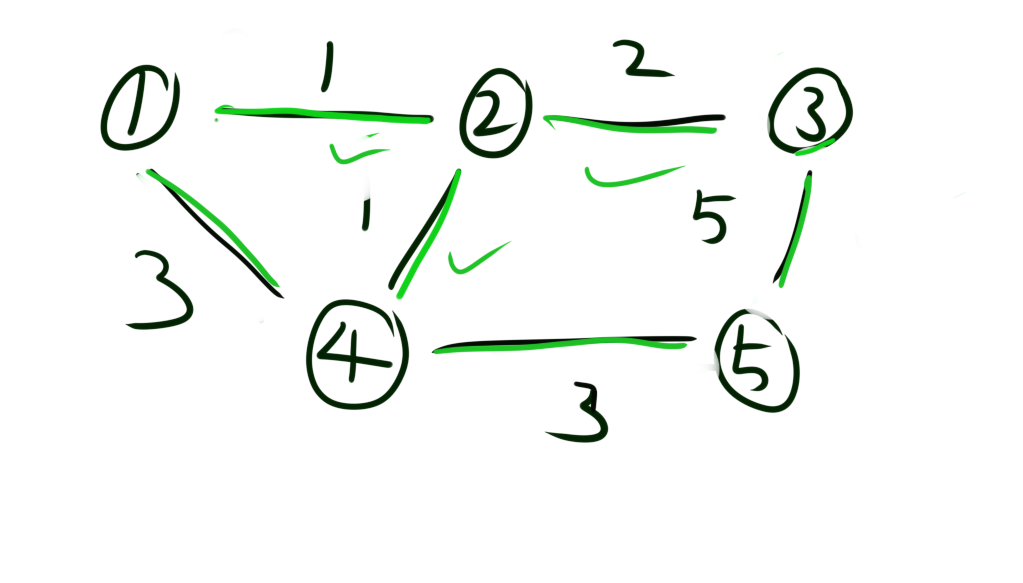
首先我们将所有的边按照权值从小到大排序。然后我们从权值最小的边开始,将这条边的两个点进行联通。如图是将1和2联通。接着再将2和4联通。就这样一直进行下去。直到所有的点都联通。
例题2
P72 【模板】最小生成树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
|
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
typedef long long ll;
struct node
{
ll u;
ll v;
ll w;
bool operator<(const node &b) const // 权值最小的优先,如果权值相同就用编号区分,编号小大无所谓
{
if (w != b.w)
{
return w < b.w;
}
if (u != b.u)
{
return u < b.u;
}
return v < b.v;
}
};
ll pre[N]; // 并查集
ll root(ll x)
{
if (pre[x] == x)
{
return x;
}
else
{
ll root_x = root(pre[x]);
pre[x] = root_x;
return root_x;
}
}
void merge(ll x, ll y)
{
pre[root(x)] = root(y);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
pre[i] = i;
}
vector<node> es; // 用vector来存边,方便排序
for (int i = 1; i <= m; i++)
{
ll u, v, w;
cin >> u >> v >> w;
es.push_back({u, v, w});
}
ll ans = 0;
sort(es.begin(), es.end());
for (auto &e : es)
{
ll u = e.u;
ll v = e.v;
ll w = e.w;
if (root(u) == root(v)) // 如果两个点已经联通了,那么这条边就不能加入到生成树中
{
continue;
}
merge(u, v); // 将这两个点联通
ans += w; // 权值累加
}
for (int i = 1; i <= n - 1; i++)
{
if (root(i) != root(i + 1)) // 最后判断一下是否所有的点都在生成树中,如果有一个点不在生成树中,那么就不构成生成树了,输出-1。
{
ans = -1;
break;
}
}
cout << ans << "\n";
return 0;
}
|
总结
通常来说,我们更倾向使用kruskal算法,因为他实现很简单
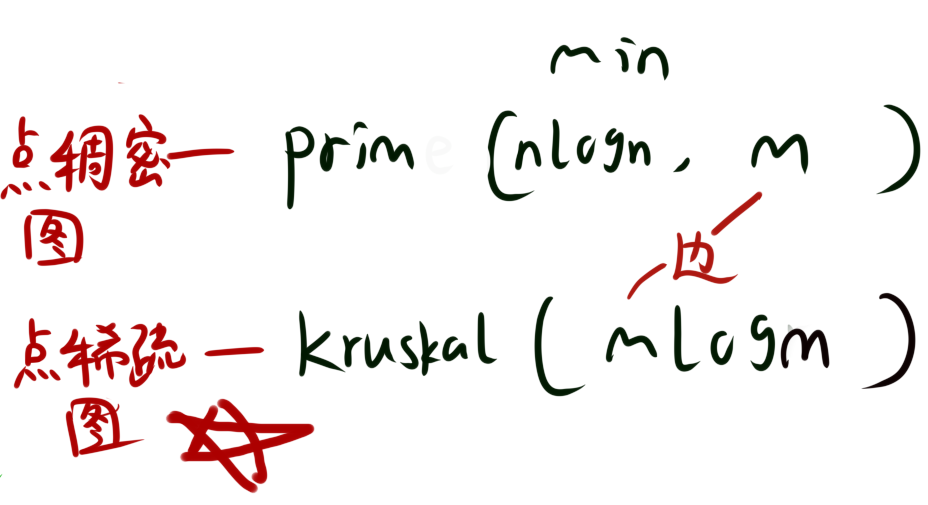
prim算法更适用于稠密图,kruskal算法更适用于稀疏图。
稠密图就是点的数量少,边的数量很多,那么一个点的邻边就很多,prim适合这种情况。
稀疏图就是点的数量多,边的数量少,那么一个点的邻边就很少,kruskal适合这种情况。
质因数分解
质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
对于质数,我们要掌握:

质数的判断
对于一个数n,我们只需要判断它是否能被$2\sim \sqrt{n}$中的数整除即可。如果能被整除,那么就不是质数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
bool isprime(int n) //质数判断
{
if (n < 2)
{
return false;
}
for (int i = 2; i <= n / i; i++)
{
if (n % i == 0)
{
return false;
}
}
return true;
}
|
因子分解
在讲质因数分解前,我们先讲一下因子分解。
P16 【模板】求N的所有因子
分析:
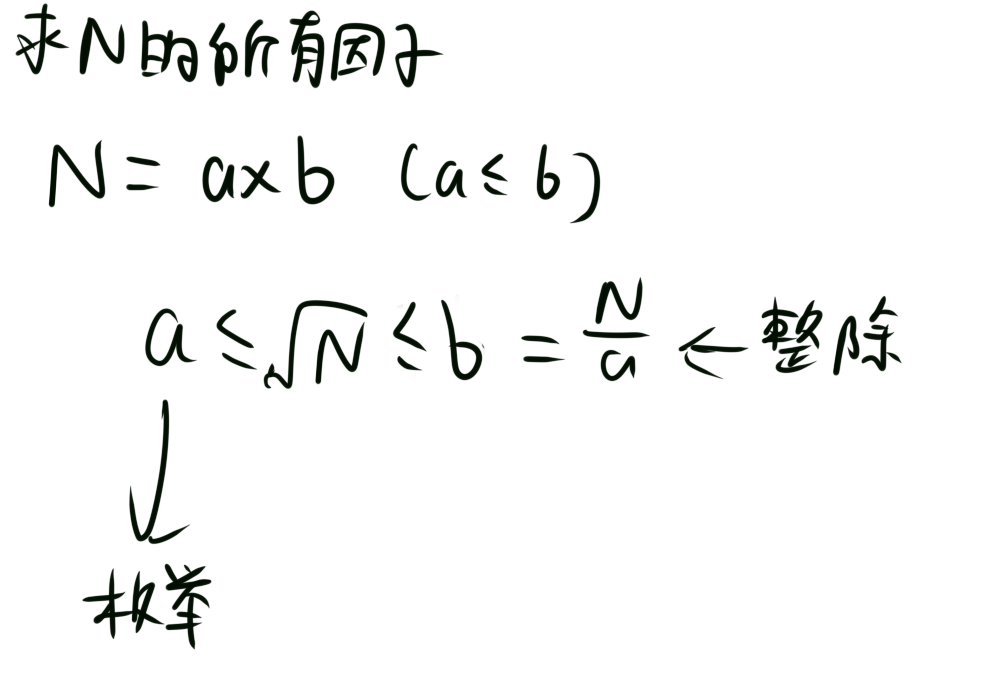
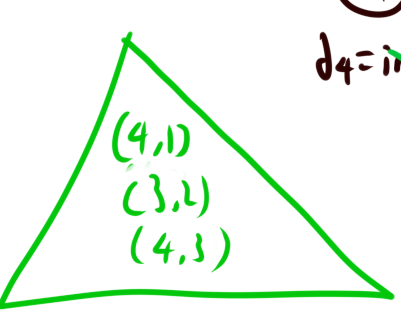
由图,我们假设一个数$N=a\times b$,那么a和b就是N的因子。
不妨设$a\leq b$,那么我们可以得到$a\leq \sqrt{N}\leq b$。
其中$b=N/a$。
那么我们只要枚举$a$,找出其中整除$N$的数即可。假如这个数为$i$,那么$b=N/i$。
我们可以用一个vector来存因子,最后排序输出即可。
注意枚举范围为$1\sim \sqrt{N}$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n;
cin >> n;
vector<ll> v;
for (ll i = 1; i <= n / i; i++)
{
if (n % i == 0)
{
// n与n/i两个因子
v.push_back(i);
if (i != n / i)
{
v.push_back(n / i);
}
}
}
sort(v.begin(), v.end());
for (auto &i : v)
{
cout << i << " ";
}
cout << "\n";
return 0;
}
|
例题
P17 【模板】求N的所有质因子
分析:
对于求N的质因子,我们可以将N分解为多个质因子的乘积。
例如:$12=2\times 2\times 3$
所以我们只要从2开始枚举,判断能否整除,如果可以整除,那么就将这个质因子加入到vector中,并且将N持续除以这个数,直到N不能再被这个数整除。如此才会保证N是由多个质因子的乘积组成的。
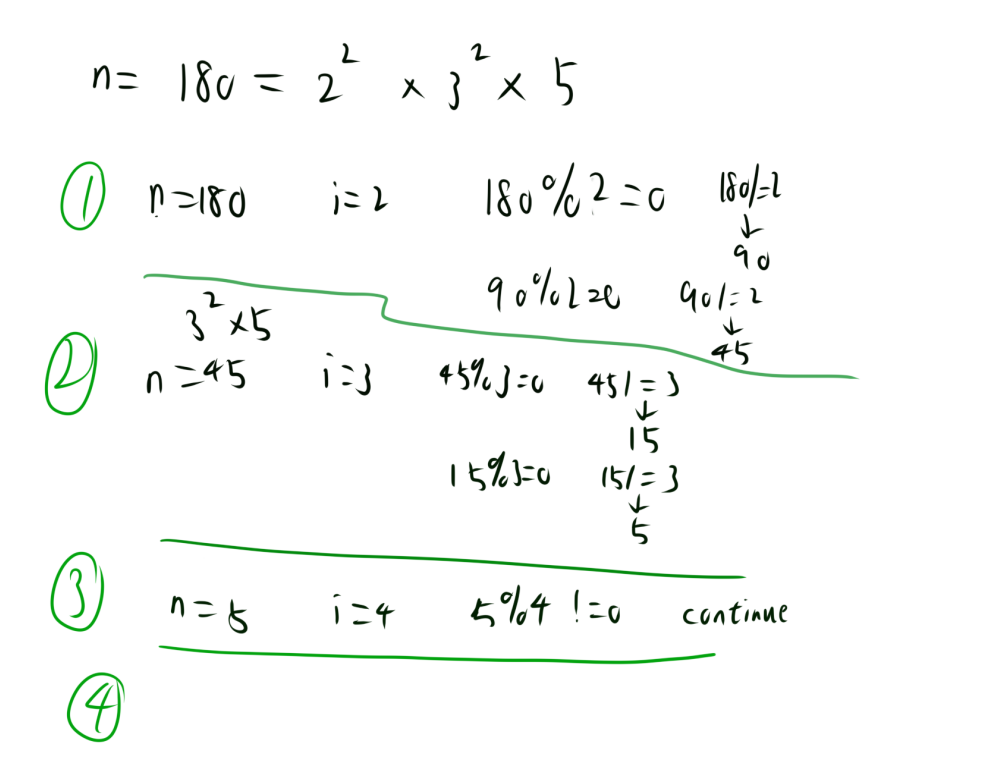
为何这样枚举得到的因子一定是质数呢?
我们可以用一个反证法来证明。
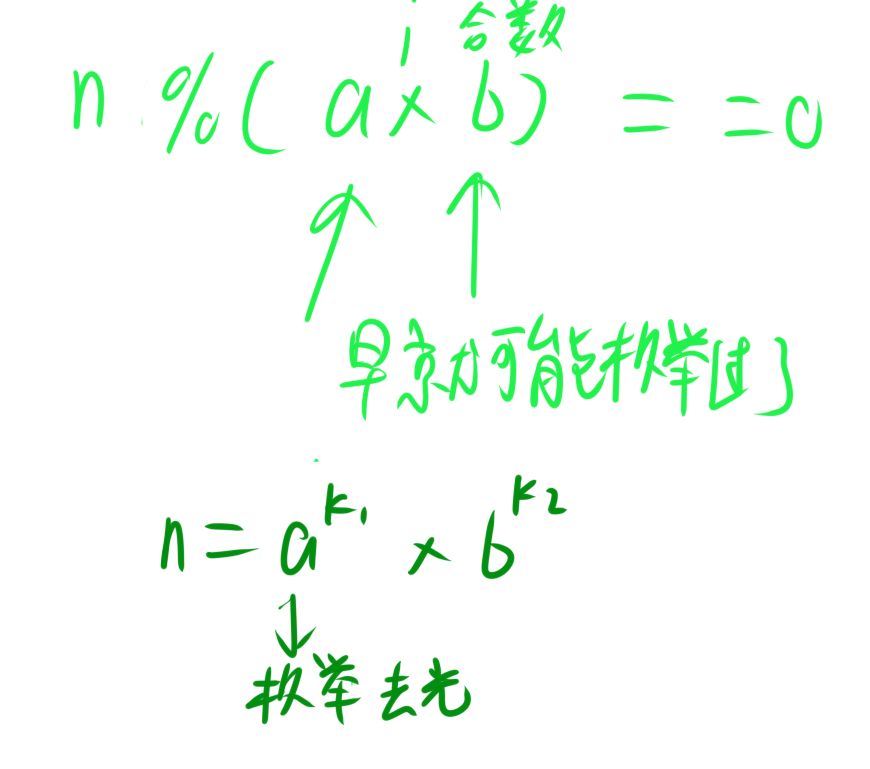
假如我们枚举到一个数$i$,但是$i$不是质数,那么$i$就可以被分解为多个质因子的乘积。即$i=a*b$为一个合数.既然$n$能被$i$整除,那么$n$也一定能被$a$和$b$整除。
但是我们的枚举是从2开始的,所以$i$的因数一定会先于i被枚举到,假设这个先被枚举到的因数为$a$,$n$一定会被$a$整除,然后a就会被除光,除剩下的$n$就不再包含了$a$了,此时再枚举到$i$,$n$也不会再被$i$整除了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
ll n;
cin >> n;
vector<ll> v;
for (ll i = 2; i <= n / i; i++) // 枚举所有质因子 i肯定要从2开始
{
if (n % i != 0)
{
continue;
}
// i为一个质因子
v.push_back(i);
while (n % i == 0)
{
n /= i; // n除去所有i
}
}
if (n > 1)
{
v.push_back(n); // 如果n>1,最后n他自己就是一个质因子
}
sort(v.begin(), v.end());
for (auto &i : v)
{
cout << i << " ";
}
cout << "\n";
return 0;
}
|