前言
学习网站:Starrycoding
离散化
离散化是一种处理数据的技巧,通俗地讲就是当我们需要处理的数据范围很大,但是数据的个数很少时,我们可以将数据的范围进行压缩,从而减少空间的占用。离散化是一种映射的思想。
将一个数组离散化,并进行查询是比较常用的应用场景。
离散化的步骤如下:
- 选择好相关点,创建原数组的副本。
- 将副本中的值从小到大排序。
- 将排序好的副本去重。
- 查找原数组的每一个元素在副本中的位置,位置即为排名,将其作为离散化后的值。(我们一般用二分查找)
例题
P63 我的很长,你算一下
分析:
根据题目,数组的下标范围是$[1,10^9]$,这么大的范围如果我们直接用数组来存储会爆内存,根本连暴力都用不了。
但是看到数据,个数只有$10^5$个,那么如果把下标作为值存储在数组中呢?
我们把这个数组叫做X,这些下标叫做相关点,X的下标叫做排名。接着我们再开一个数组Y,Y的下标和X的下标一一对应,而Y的值存储的是原数组的值,也可以用来加减了。
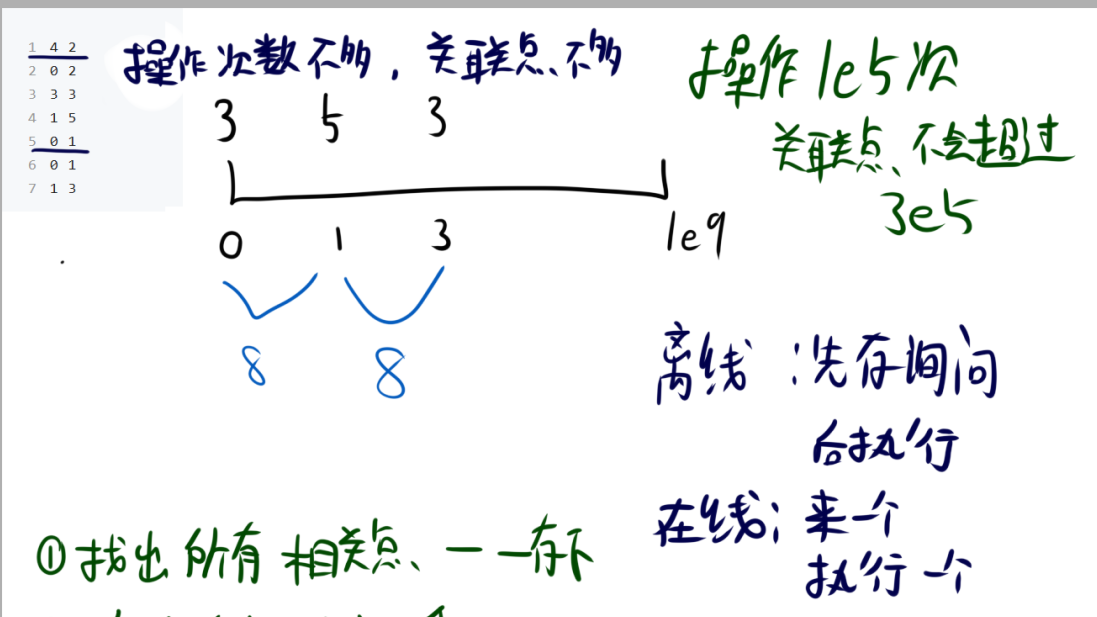
这样通过两个数组,我们就可以通过排名来查询原数组的值了。
总结得到这样的映射关系:排名–>原数组的下标–>原数组的值
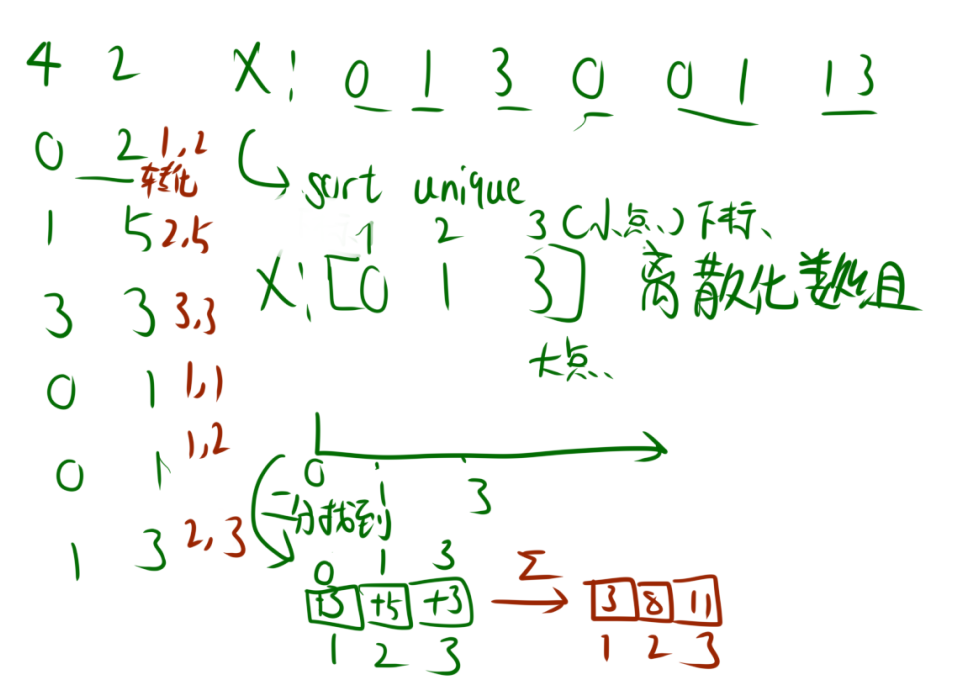
所以我们可以将数组的下标进行离散化,然后用数组来存储。那么我们就有办法存储相关点了,也可以再用二分得到相关点的排名。

这里要注意,既然离散化的是下标,那么q次询问中的l和r也要记录进X中.这样才能得到排名。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e5 + 9;
ll arr[N];
vector<int> X;
struct Q // 存放操作和询问
{
ll a, b;
} add[N], que[N];
ll getidx(int x)
{
/*lower_bound下边界 up_bound 上边界
由于计算机区间习惯左闭右开,所以lower_bound返回第一个等于x的元素(假如有),up_bound返回第一个大于x的元素
<x, <x, <x, [x, x, x, >x) ,>x
lower_bound找出数组中第一个大于等于x元素的迭代器,up_bound返回的是第一个严格大于给定值的元素的迭代器。*/
return lower_bound(X.begin(), X.end(), x) - X.begin() + 1;
// 返回值范围是[1,X.size()]
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, q;
cin >> n >> q;
for (int i = 1; i <= n; i++)
{
ll x, w;
cin >> x >> w;
X.push_back(x);
add[i] = {x, w};
}
for (int i = 1; i <= q; i++)
{
ll l, r;
cin >> l >> r;
X.push_back(l);
X.push_back(r);
que[i] = {l, r};
}
// 排序去重
sort(X.begin(), X.end());
X.erase(unique(X.begin(), X.end()), X.end());
for (int i = 1; i <= n; i++)
{
ll x = getidx(add[i].a);
ll w = add[i].b;
arr[x] += w;
}
// 前缀和
for (int i = 1; i <= X.size(); i++)
{
arr[i] += arr[i - 1];
}
for (int i = 1; i <= q; i++)
{
ll l = getidx(que[i].a);
ll r = getidx(que[i].b);
cout << arr[r] - arr[l - 1] << "\n";
}
return 0;
}
|
树状数组

树状数组是一种支持单点修改,区间查询和区间修改(区间修改运用了差分)的,代码量小的数据结构。树状数组简单来说,算是一种高级前缀和。
假如有个数组$a$,我们想得到这个数组的前缀和很简单,只需要用一个数组$sum$来存储前缀和就可以了。但是,如果我们要修改数组$a$中的一个元素,然后马上查询那个区间的和,那么我们$sum$就要重新进行前缀和再输出,这样的话,时间复杂度就会很高。
想解决这种在线的单点修改,就得使用树状数组。
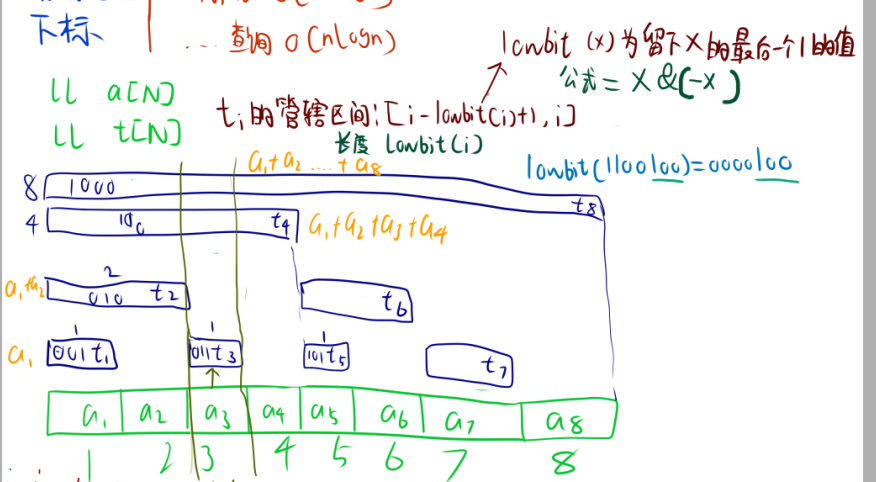
如图,开一个数组$t$视为树状数组,$t_1$存的是$a_1$,$t_2$存的是$a_1+a_2$,$t_4$存的是$a_1+a_2+a_3+a_4$,$t_8$存的是$a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8$。别的也是如图一一对应的。
这样存储会带来什么性质?
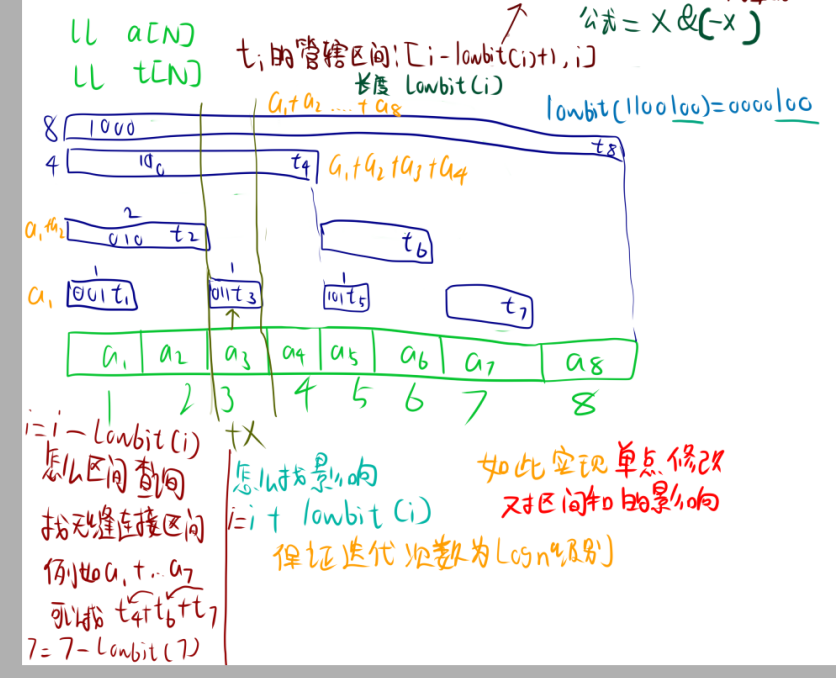
我们把$t$存的数的区间称为管辖区间。这个管辖区间为$[i-lowbit(i)+1,i]$。长度为lowbit(i)。
什么是lowbit(i)?
lowbit(i)是i的二进制表示中最低位的1所代表的数值。
例子:lowbit(1100100)=0000100
lowbit公式:lowbit(i)=i&(-i)
我们把这个公式代入到例子看,$t_8$长度就为8,它的管辖区间为$[8-lowbit(8)+1,8]=[1,8]$。因此他是$a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8$。
那么我们如何进行单点修改呢?
可以看出,如果我们对$a_3$进行修改,那么$t_3,t_4,t_8$都要进行修改。这样的影响是有规律的。
我们可以发现,3+lowbit(3)=4,4+lowbit(4)=8,所以我们可以用一个循环来实现单点修改。

那么接下来我们就要实现区间查询了。
虽然$t_8$把全部元素包括了,但假如我们要的和是部分的话该怎么办呢?例如,我们要的是$a_1$到$a_7$的和。观察一下,可以发现$a_1$到$a_7$可以分为$t_4$+$t_6$+$t_7$。
这种无缝连接的块也是有规律的。
我们可以发现,7-lowbit(7)=6,6-lowbit(6)=4,所以我们可以用一个循环来实现区间查询。

最后,如何初始化树状数组呢?
我们可以把$t$数组初始化为0,然后用单点修改来实现初始化,就可以了。(和差分的思想有点类似)。
例题1
P40 【模板】树状数组(单点修改)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9;
typedef long long ll;
ll a[N], t[N];
int n, q;
int lowbit(int x)
{
return x & -x;
}
void update(int k, ll x)//单点修改,也负责初始化
{
for (int i = k; i <= n; i += lowbit(i))
{
t[i] += x;
}
}
ll getsum(int k)//区间查询求前缀和
{
ll ans = 0;
for (int i = k; i > 0; i -= lowbit(i))
{
ans += t[i];
}
return ans;
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
// 初始化树状数组
for (int i = 1; i <= n; i++)
{
update(i, a[i]);
}
// 操作
for (int i = 1; i <= q; i++)
{
int x;
cin >> x;
if (x == 1)
{
int k;
ll v;
cin >> k >> v;
update(k, v);
}
else
{
int l, r;
cin >> l >> r;
ll ans = 0;
ans = getsum(r) - getsum(l - 1);
cout << ans << "\n";
}
}
return 0;
}
|
接下来讲区间修改。
如果是区间修改,离线的话我们可以用差分来实现,时间复杂度比树状数组更加优秀。
但是,如果是要求在线的区间修改,即修改一次,就要我们出一次值,我们就必须用树状数组来实现了。
树状数组想要实现区间修改,就是从维护普通的前缀和变成维护差分数组的前缀和。

如图,我们得出推广公式:
$$\sum_{i=1}^{r}a_i=\sum_{i=1}^{r} (r+1)d_i-\sum_{i=1}^{r}id_i$$那么我们用两个树状数组来维护这两个差分前缀和就可以了。
我们可以先初始化出差分数组$d$,然后用树状数组来维护$d$的前缀和。也可以直接就用树状数组来得出$d$的前缀和。
例题2
P41 树状数组(区间修改)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9;
typedef long long ll;
ll a[N], dt[N], dti[N];
int n, q;
int lowbit(int x)
{
return x & -x;
}
void update(int k, ll x) //单点修改,一次对两个树状数组进行修改
{
for (int i = k; i <= n; i += lowbit(i))
{
dt[i] += x;
dti[i] += k * x; //注意这里是k*x,不是i*x
}
}
ll getsum(int k) //区间查询,运用刚才的公式得出
{
ll ans = 0;
for (int i = k; i > 0; i -= lowbit(i))
{
ans += (k + 1) * dt[i] - dti[i];
}
return ans;
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
// 初始化树状数组
for (int i = 1; i <= n; i++)
{
update(i, a[i]);
update(i + 1, -a[i]); //根据差分,我们这样单点修改就可以实现区间修改了
}
// 操作
for (int i = 1; i <= q; i++)
{
int x;
cin >> x;
if (x == 1)
{
int l, r;
ll v;
cin >> l >> r >> v;
update(l, v); //区间修改
update(r + 1, -v);
}
else
{
int l, r;
cin >> l >> r;
ll ans = 0;
ans = getsum(r) - getsum(l - 1);
cout << ans << "\n";
}
}
return 0;
}
|
附加题
P31 求逆序对个数
题面:
给定一个长度为$n$的数组$a$,求$a$的逆序对个数。
逆序对的定义是一个二元组$(a_i,a_j)$,满足:$i<j$且$a_i>a_j$。
输入格式:
一个整数n.($1\leq n\leq 2\times10^5$)
一个长度为$n$的数组$a$。($1\leq a_i\leq 10^9$)
输出格式:
一个整数,表示逆序对的个数。
分析:
此题求解逆序对,可以使用权值数组来求解,权值数组其实就是一个桶,桶的下标就是数组的值,桶的元素就是数组的值的个数。

如图,我们把2,3,1,1,6依次归入桶中,先进2,$a_2$值为1,然后遍历$a_2$之后的桶,发现桶里面个数都为0,说明2之前没有比2大的。然后进3,然后进1,发现有两个逆序对,再进1,发现有两个逆序对,如此结束。
接着我们发现这样虽然找得到,但时间复杂度很高,而且(10^9)的范围太大,所以我们需要用离散化来优化。
至于如何优化时间复杂度,可以这样逆向的求解,同样是2,3,1,1,6,2进桶之前,先判断下所有桶里面的元素个数,然后再减去其中比2小的元素个数,这样就可以得到2之前的逆序对个数。
这样的话就要有个前缀和,我们可以用树状数组来实现(时间复杂度优秀,总共$O(nlogn)$)。并且建立在离散化处理的数组的基础上。
树状数组<–排名<–值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 9;
typedef long long ll;
ll a[N], t[N];
vector<int> X;
int getidx(int x)
{
return lower_bound(X.begin(), X.end(), x) - X.begin() + 1;
}
int lowbit(int x)
{
return x & -x;
}
int getsum(int k)
{
int res = 0;
for (int i = k; i > 0; i -= lowbit(i))
{
res += t[i];
}
return res;
}
void update(int k, int x)
{
for (int i = k; i <= X.size(); i += lowbit(i))
{
t[i] += x;
}
}
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
X.push_back(a[i]);
}
// 排序去重
sort(X.begin(), X.end());
X.erase(unique(X.begin(), X.end()), X.end());
/*
树状数组是建立在离散化数组上的
getsum(X.size())返回当前位置之前的所有元素的和
getsum(getidx(a[i]))返回当前位置之前小于等于a[i]的元素的个数
两者相减即为比 a[i] 大的元素的数量。
*/
ll ans = 0;
for (int i = 1; i <= n; i++)
{
ans += 1ll * getsum(X.size()) - getsum(getidx(a[i]));
update(getidx(a[i]), 1);
}
cout << ans << "\n";
return 0;
}
|










