前言
学习网站:Starrycoding
前缀和是一种重要的预处理,能大大降低查询的时间复杂度,而差分则是一种和前缀和相对的策略。
前缀和
前缀和预处理可以帮助我们在$O(1)$的时间复杂度内求出$a$数组中任意区间$[l,r]$的和,即$a_l+a_{l+1}+a_{l+2}+…+a_r$,而不需要每次都遍历一遍区间,这大大提高了查询的效率。
前缀和通常用数组来实现,假设我们有一个数组a,那么我们可以用数组b来表示a的前缀和,即
$$b_1=a_1,b_2=a_1+a_2,b_3=a_1+a_2+a_3....$$如此循环,直到加到$b_n$,那么$b_n$就是a的所有元素之和

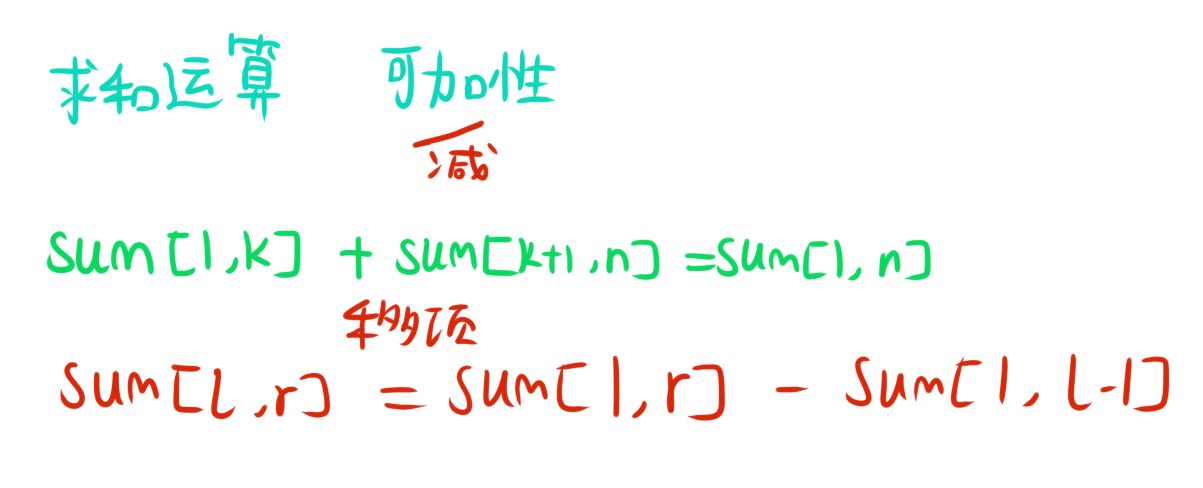
一维前缀和题目:P7 【模板】前缀和
模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t, n, q;
cin >> t;
while (t--)
{
vector<ll> arr(100010);
vector<ll> sum(100010);
cin >> n >> q;
for (int i = 1; i <= n; i++)
{
cin >> arr[i];
}
sum[1] = arr[1];
for (int i = 2; i <= n; i++)
{
sum[i] = sum[i - 1] + arr[i]; // 前缀和处理
}
int l = 0, r = 0;
while (q--)
{
cin >> l >> r;
ll res = sum[r] - sum[l - 1];
cout << res << '\n';
}
}
return 0;
}
|
补充:二维前缀和
二维前缀和思想和一维的一致,只不过我们需要二维数组来实现,并且初始化也会有所不同
二维前缀和题目:P15 【模板】二维前缀和
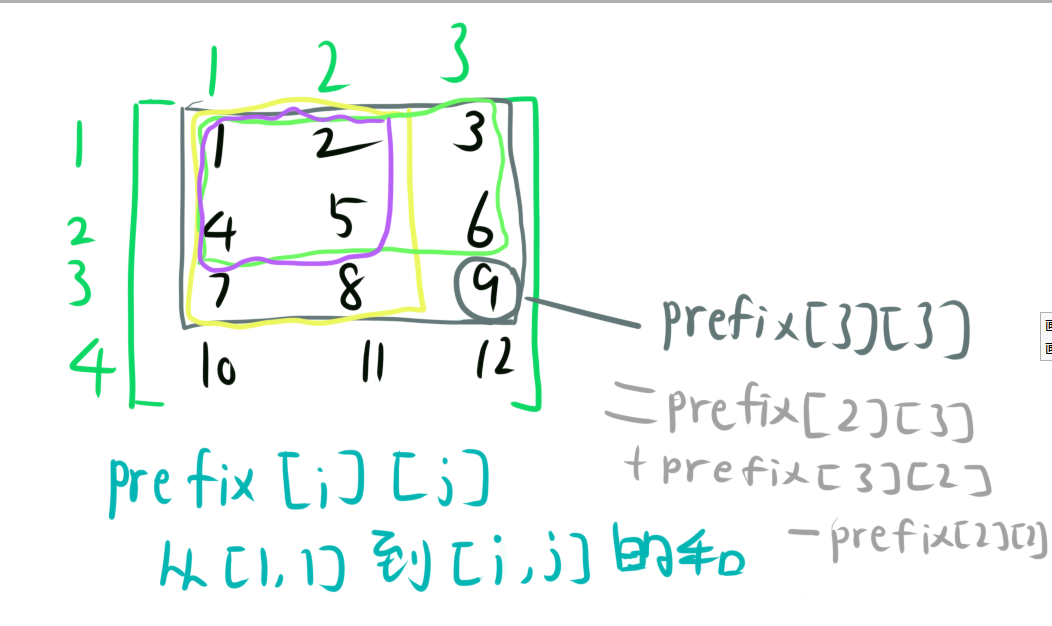
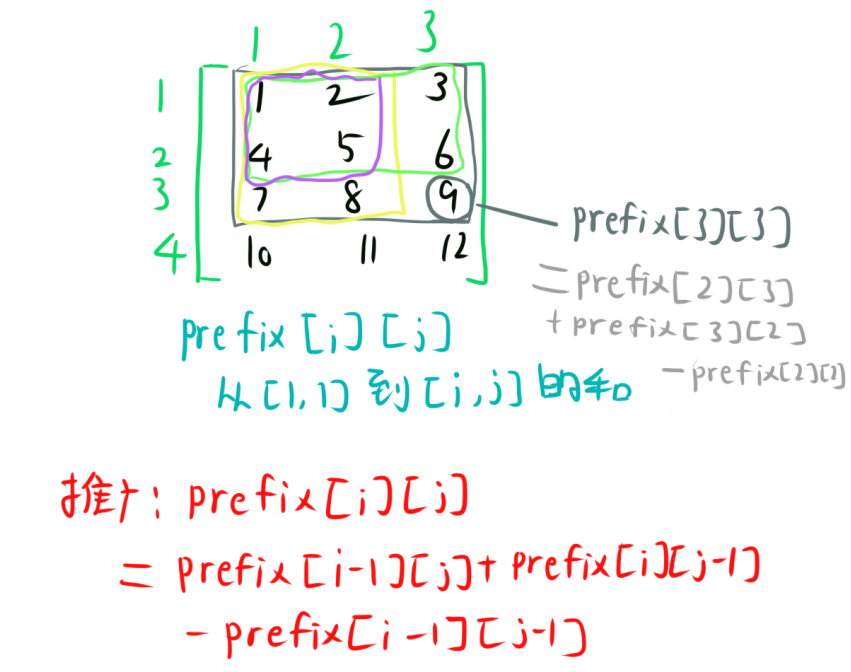
如图即为二维前缀和的初始化(少加了$a_{3,3}$),我们假设一个二维数组a,我们用二维数组b来表示a的二维前缀和,即
$$b_{3,3}=b_{2,3}+b_{3,2}-b_{2,2}+a_{3,3}$$这涉及了一点递归(递推)的思想(可以自己从1,1开始推一下)
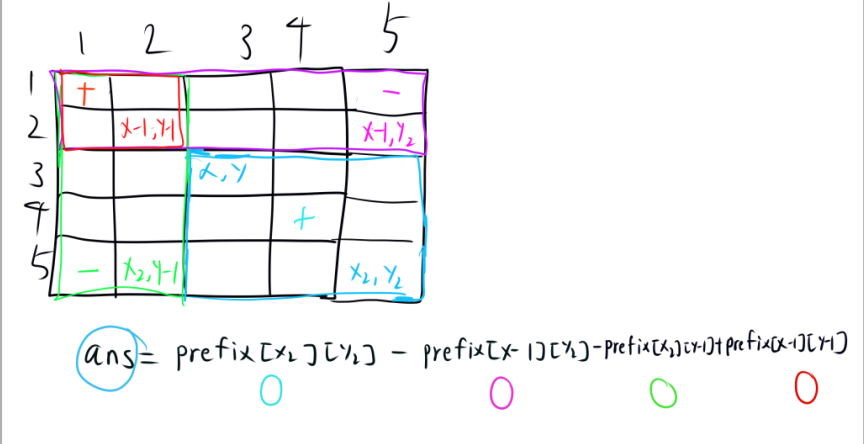
模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1200;
int g[N][N];
ll prefix[N][N];
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> g[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + g[i][j];
}
}
int x_l, y_l, x_r, y_r;
while (q--)
{
cin >> x_l >> y_l >> x_r >> y_r;
ll res = 0;
res = prefix[x_r][y_r] + prefix[x_l - 1][y_l - 1] - prefix[x_r][y_l - 1] - prefix[x_l - 1][y_r];
cout << res << '\n';
}
return 0;
}
|
差分
差分的作用是在$O(n)$ (n为修改数值次数)的时间复杂度内,将$a$数组中$[l,r]$区间的所有数加上一个数$c$,而不需要每次都遍历一遍区间,这同样也是一种预处理从而增加效率的方式。
需要注意的是通过差分实现区间修改,是一种静态维护,也就是说我们只能在修改完才能询问,而无法边修改边询问。
假设我们有一个数组a,用数组b来表示a的差分,即
$$b_1=a_1,b_2=a_2-a_1,b_3=a_3-a_2....$$这里我们可以发现一个规律,如果得出b数组的前缀和,那么就有
$$b_1+b_2+...b_i=a_1+a_2-a_1+...a_i-a_{i-1}$$
即
$$b_1+b_2+...b_i=a_i$$我们由此得出差分的性质就是可以通过差分的前缀和来得到原数组的其中一个元素。
基于差分的这个性质,我们就可以用差分来实现静态的区间修改

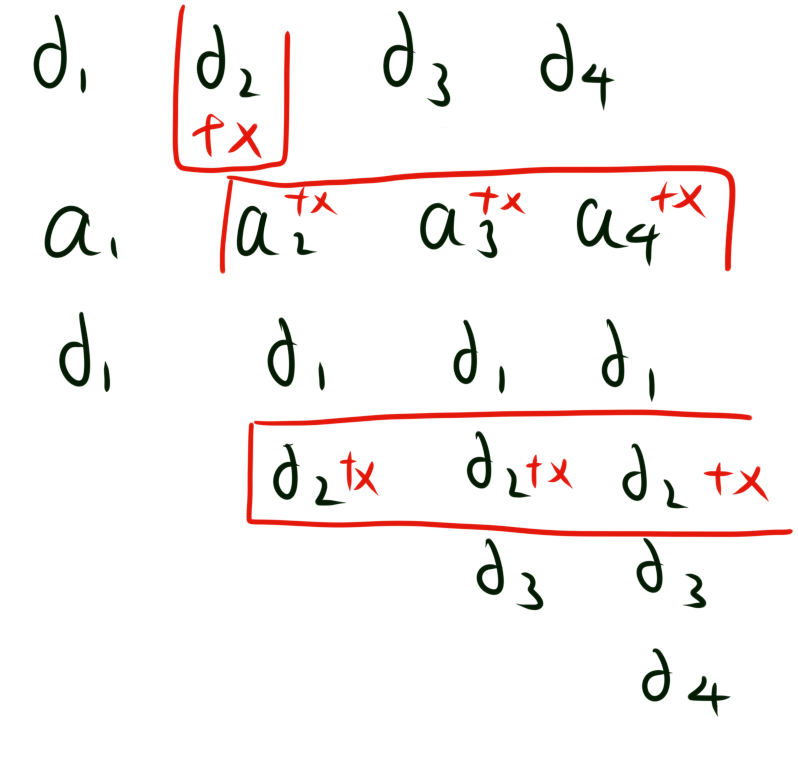
如果我们给差分数组d中的$d_2$加上一个数$x$,那么用前缀和还原时,就会发现从$a_2$开始所有的数都加上了$x$
那假如我们要给$[2,3]$区间加上一个数$x$呢?
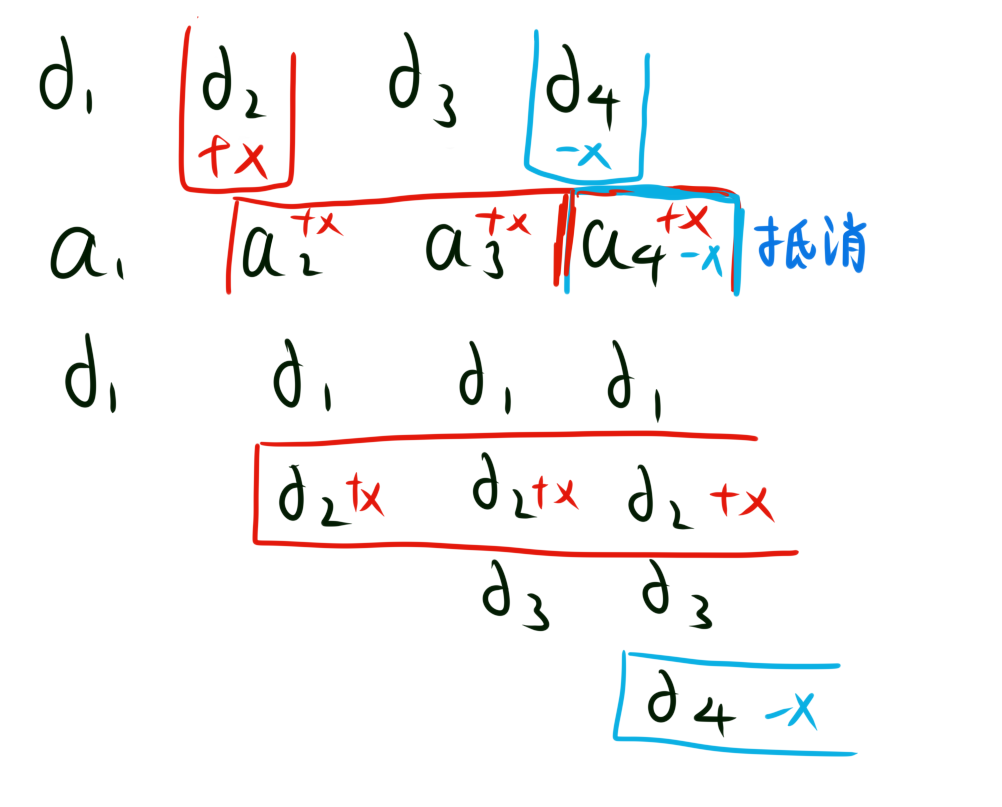
如图,只要在$d_2$加上$x$,在$d_4$减去$x$即可
由此,我们得出了差分的区间修改的公式
若想修改$[l,r]$区间的数,只需在差分数组上做如下操作
$$d_l+=x,d_{r+1}-=x$$此时,我们再回过头看开头时我们是如何表示差分的,就可以发现其实他们也遵循了这个修改区间的公式,只不过他们的区间很小,是$[1,2]$,$[2,3]$,$[3,4]$…以此类推下去。
注:一维差分数组可以直接用$d_i=a_i-a_{i-1}$来表示,而二维差分数组我们一般用上面的公式来初始化

一般来说,差分题目在修改完区间后,就会询问区间和,所以还会需要再进行一次前缀和
一维差分题目:P8 【模板】差分
模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 9;
ll arr[N];
ll differ[N];
ll prefix[N];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, p, q;
ll x = 0, l = 0, r = 0;
cin >> n >> p >> q;
for (int i = 1; i <= n; i++)
{
cin >> arr[i];
}
for (int i = 1; i <= n; i++)
{
differ[i] = arr[i] - arr[i - 1]; // 差分处理
}
while (p--)
{
cin >> l >> r >> x;
differ[l] += x;
differ[r + 1] -= x; // 修改区间
}
for (int i = 1; i <= n; i++)
{
arr[i] = arr[i - 1] + differ[i]; // 通过差分还原数组,并且数据经过修改
}
for (int i = 1; i <= n; i++)
{
prefix[i] = prefix[i - 1] + arr[i]; // 前缀和
}
while (q--)
{
cin >> l >> r;
ll res = 0;
res = prefix[r] - prefix[l - 1];
cout << res << '\n';
}
return 0;
}
|
补充:二维差分
二维差分的特点就如前面所说,我们初始化需要使用公式才会更有助于理解
二维差分题目:P50 【模板】二维差分
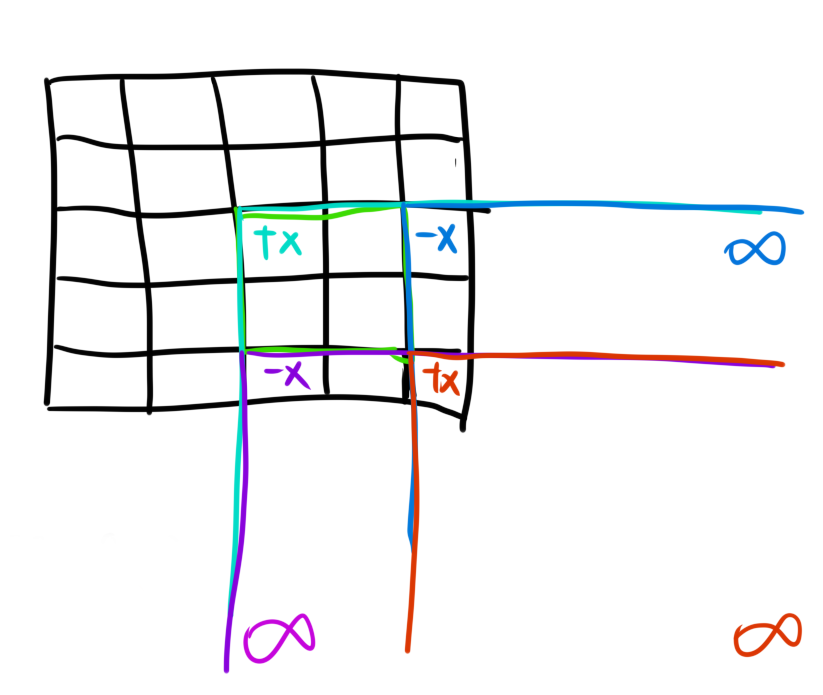 由图,我们先假设我们已经初始化了一个二维差分数组,图上这些格子内部便是坐标点,现在我们要给$[2,2]$到$[4,4]$区间加上一个数$x$
就应该把$d_{2,2}$加上$x$,$d_{4+1,2}-=x$,$d_{2,4+1}-=x$,$d_{4+1,4+1}+=x$
由图,我们先假设我们已经初始化了一个二维差分数组,图上这些格子内部便是坐标点,现在我们要给$[2,2]$到$[4,4]$区间加上一个数$x$
就应该把$d_{2,2}$加上$x$,$d_{4+1,2}-=x$,$d_{2,4+1}-=x$,$d_{4+1,4+1}+=x$
同理,我们初始化也可以如此操作
那么我们就可以得出二维差分的区间修改公式
假设我们修改的区间为$[x_1,y_1],[x_2,y_2]$
则有以下公式
$$d_{x_1,y_1}+=x,d_{x_2+1,y_1}-=x,d_{x_1,y_2+1}-=x,d_{x_2+1,y_2+1}+=x$$模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
#include <bits/stdc++.h>
using namespace std;
const int N = 1100;
int arr[N][N];
int differ[N][N];
int prefix[N][N];
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> arr[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
differ[i][j] += arr[i][j]; // 这里差分初始化用的原理和下面一样
differ[i + 1][j] -= arr[i][j]; // 和下面不一样的是因为就只要一个格子变,所以左上右下的坐标都是(i,j)
differ[i][j + 1] -= arr[i][j];
differ[i + 1][j + 1] += arr[i][j];
}
}
int a, b, c, d, v;
while (q--)
{
cin >> a >> b >> c >> d >> v;
differ[a][b] += v;
differ[a][d + 1] -= v;
differ[c + 1][b] -= v;
differ[c + 1][d + 1] += v;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
arr[i][j] = arr[i - 1][j] + arr[i][j - 1] - arr[i - 1][j - 1] + differ[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cout << arr[i][j] << " ";
}
cout << '\n';
}
return 0;
}
|
附加题
涉及:?运算符的应用,最大子段和
题目p35.鼠鼠我鸭
分析:题目将重量分为两种类型,一种可以算进答案,一种不行,并且,我们可以使用一次操作来变更一段区间$[l,r]$的类型,我们可以用一个bool数组来记录,0代表不行,1代表可以,既然要求最大值,那么我们可以先把未改变时的答案求出来,接着再求更改时的增加量。

如图,想要实现这个功能可以运用?运算符(不过此题也可以直接乘以bool数组来实现)
接着,观察题目不难发现,更改后的答案绝对是要>=未改变时的答案的,所以我们只需要比较更改后的增加量和0的大小即可。
此时要求出这个增加量,我们可以先初始化一个全变更的数组(偏移量数组),接着在这个数组中求出最大子段和即可。
这里有两种求最大子段和的方法:
- 前缀和求法

我们将偏移量数组求前缀和,然后用$prefix_r-prefix_{l-1}$来求出最大子段和(要使fix最大,就要使$prefix_{l-1}$在区间$[0,r-1]$为确定的最小值,然后再枚举$prefix_r$即可)
1
2
3
4
5
6
7
8
9
10
11
12
13
|
ll minn = 0;
// minn默认为0是因为prefix[]中的元素从1开始,而我们要找prefix[l-1]的最小值是可以超出下标的,
// 所以绝对会找到prefix[0],则minn可以取0
for (int i = 1; i <= n; i++)
{
prefix[i] = prefix[i - 1] + a[i] * (w[i] ? -1 : 1);
}
ll fix = 0;
for (int i = 1; i <= n; i++) // 求偏移量的最大字段和方法(使用前缀和)
{
fix = max(fix, prefix[i] - minn);
minn = min(minn, prefix[i]);
}
|
- 贪心求法

如果mx<0,则将其重置为0,然后再加上a[i]即可,最后再用mx更新答案即可。
思想:如果当前的字段和为负数,那么下一次加数字时,我们选择重置为0再加绝对会比直接加的数字大
1
2
3
4
5
|
ll mx = 0;
for (int i = 1; i <= n; i++)
{
mx = max(0ll, mx + a[i] * (w[i] ? -1 : 1));
}
|
题目答案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 9;
ll a[N];
bool w[N];
ll prefix[N];
int n;
int main(void)
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while (t--)
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> w[i];
}
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
ll sum = 0;
ll ess = 0;
ll minn = 0; // minn默认为0是因为prefix[]中的元素从1开始,而我们要找prefix[l-1]的最小值是可以超出下标的,
// 所以绝对会找到prefix[0],则minn可以取0
for (int i = 1; i <= n; i++)
{
ess += a[i] * w[i];
}
for (int i = 1; i <= n; i++)
{
prefix[i] = prefix[i - 1] + a[i] * (w[i] ? -1 : 1);
}
ll fix = 0;
for (int i = 1; i <= n; i++) // 求偏移量的最大字段和方法(使用前缀和)
{
fix = max(fix, prefix[i] - minn);
minn = min(minn, prefix[i]);
}
ll ans = ess + fix;
cout << ans << '\n';
}
}
|

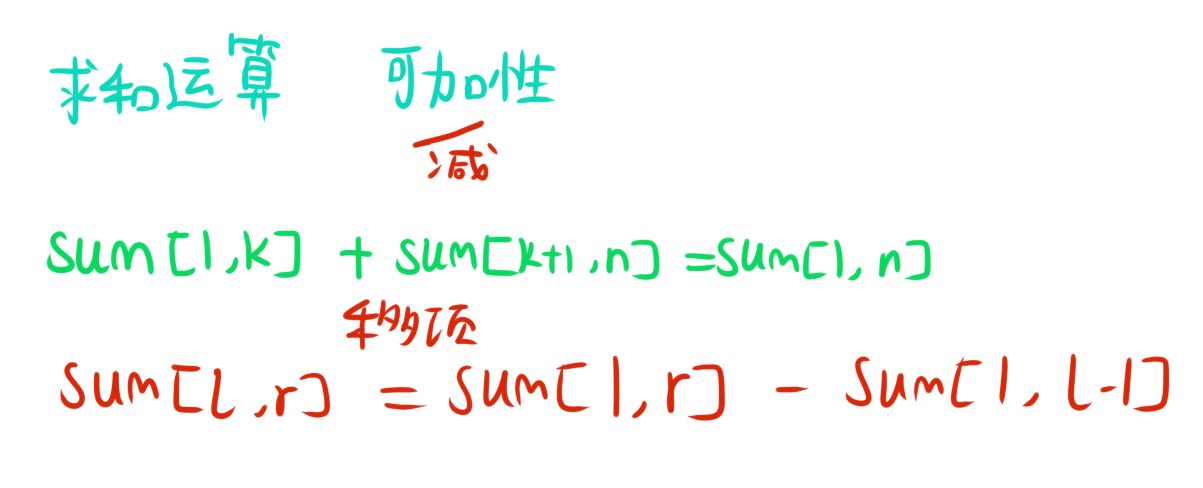


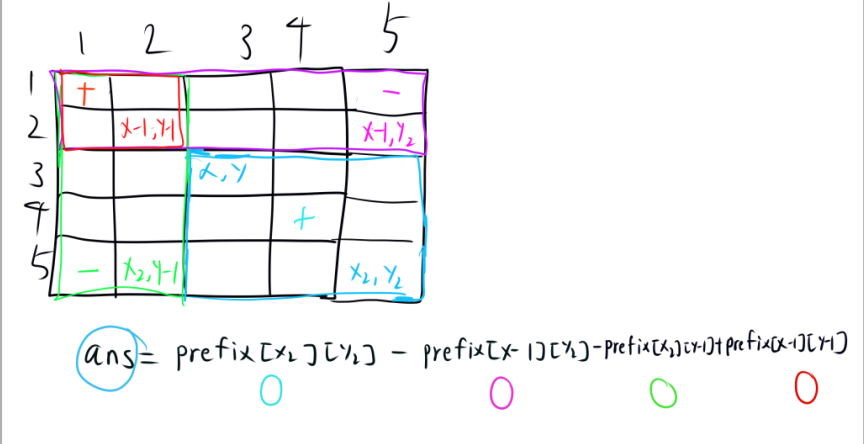

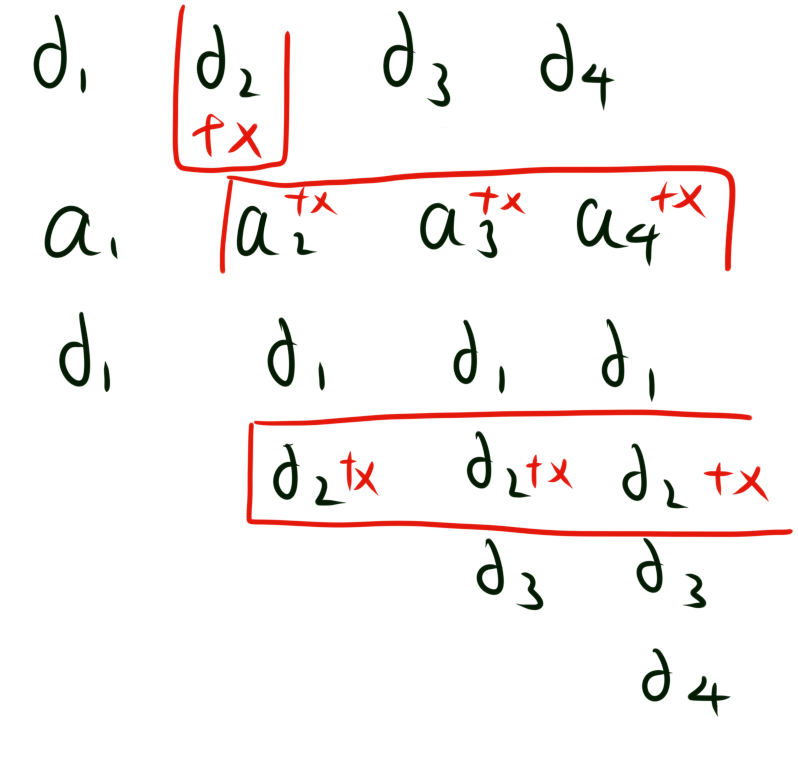


 由图,我们先假设我们已经初始化了一个二维差分数组,图上这些格子内部便是坐标点,现在我们要给$[2,2]$到$[4,4]$区间加上一个数$x$
就应该把$d_{2,2}$加上$x$,$d_{4+1,2}-=x$,$d_{2,4+1}-=x$,$d_{4+1,4+1}+=x$
由图,我们先假设我们已经初始化了一个二维差分数组,图上这些格子内部便是坐标点,现在我们要给$[2,2]$到$[4,4]$区间加上一个数$x$
就应该把$d_{2,2}$加上$x$,$d_{4+1,2}-=x$,$d_{2,4+1}-=x$,$d_{4+1,4+1}+=x$


